Cho hàm số y = a x 3 + b x 2 + c x + d ( a ≠ 0 ) có đồ thị
như hình vẽ. Khẳng định nào sau đây đúng?
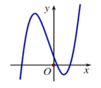
A. a > 0, d > 0 ; b < 0, c < 0.
B. a < 0, b < 0, c < 0 ; d > 0
C. a > 0, c > 0, d > 0 ; b < 0.
D. a > 0, b > 0, d > 0 ; c < 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ta có: ![]()
Dựa vào đồ thị:
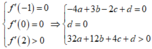

![]()
Dựa vào đồ thị, ta cũng có: ![]()
Từ (1),(2) suy ra a + c > 4a + c > 0.

Đồ thị hàm số có tiệm cận đứng x = a > 0; tiệm cận ngang y = b > 0
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên
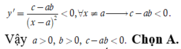

Chọn D
Ta có
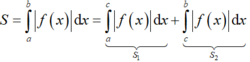
Vì f(x) < 0, ∀ x ∈ a ; c nên |f(x)| = –f(x).
Do đó, S 1 = - ∫ a c f x d x .
Tương tự, f(x) > 0, ∀ x ∈ a ; c nên |f(x)| = f(x).
Do đó, S 2 = ∫ c b f x d x .
Vậy S = - ∫ a c f x d x + ∫ c b f x d x .
Đáp án D
Đồ thị hàm số đi từ dưới lên ⇒ a < 0 .
Đồ thị có 2 điểm cực trị đạt được tại hoành độ trái dấu và tổng nhỏ hơn 0 nên ta có c a < 0 ⇒ c < 0
Và – b a 0 ⇒ b 0
Đồ thị hàm số cắt trục tung tại điểm dương ⇒ d > 0 .