Có bao nhiêu số nguyên m ∈ - 20 ; 20 để phương trình 9 x - 3 x + 1 + m 2 + 9 x - 8 . 3 x + 2 m = 0 có đúng hai nghiệm thực phân biệt?
A. 19
B. 23
C. 21
D. 22
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lưu ý rằng \(x^2+2>0\) với mọi x, do đó \(x^2+2=\left|x^2+2\right|\):
\(y=\left(x^2+2\right)\left|x^2-m\right|=\left|\left(x^2+2\right)\left(x^2-m\right)\right|\)
Tới đây là 1 bài biện luận cực trị của hàm trị tuyệt đối trùng phương khá cơ bản:
\(g\left(x\right)=\left(x^2+2\right)\left(x^2-m\right)=x^4-\left(m-2\right)x^2-2m\)
\(g'\left(x\right)=4x^3-2\left(m-2\right)x=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=\dfrac{m-2}{2}\end{matrix}\right.\)
Do \(g\left(x\right)=0\Leftrightarrow\left(x^2+2\right)\left(x^2-m\right)=0\Leftrightarrow x^2=m\) có tối đa 2 nghiệm
Đồng thời \(g'\left(x\right)=0\) có tối đa 3 nghiệm
\(\Rightarrow\) Hàm có 5 cực trị khi và chỉ khi \(g\left(x\right)=0\) có 2 nghiệm pb đồng thời \(g'\left(x\right)=0\) có 3 nghiệm pb và các nghiệm này ko trùng nhau
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\dfrac{m-2}{2}>0\\m\ne\dfrac{m-2}{2}\end{matrix}\right.\) \(\Leftrightarrow m>2\)
có đứa bạn mình làm theo hướng là đạo hàm ngay từ đầu, nếu làm cách đó thì có nhanh hay dễ tư duy hơn không???

Chọn đáp án B.
![]()
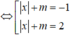
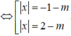
Phương trình có bốn nghiệm thực phân biệt
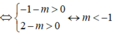
![]()
Vậy có tất cả 18 số nguyên thoả mãn.

Có bao nhiêu số nguyên tố nhỏ hơn 20
Có 8 số nguyên tố nhỏ hơn 20


Có 4 phân số bằng phân số -15/20
Đó là : -3/4 ; -6/8 ; -9/12 ; -12/16
Ủng hộ nha
Bạn ơi có 4 phân số bằng phân số -15/20 đó là:
-3/4; -6/8; -9/12; -12/16.
Nhớ kết bạn với mình nha Nalumi Likika


program hoc24;
n: string[20];
k,i,t,d,d1: byte;
code: integer;
begin
write('Nhap so K: '); readln(k);
write('Nhap so nguyen N: '); readln(n);
d:=0; d1:=0;
for i:=1 to k do
begin
val(n[i],t,code);
if t mod 2=0 then d:=d+1 else d1:=d1+1;
end;
writeln('Co ',d,' chu so chan');
write('Co ',d1,' chu so le');
readln
end.
Đặt phương trình trở thành:
phương trình trở thành: 
Đặt tiếp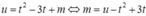 phương trình trở thành:
phương trình trở thành:
Với mỗi t > 0 cho duy nhất một nghiệm x = log 3 t phương trình có đúng hai nghiệm thực phân biệt khi và chỉ khi (*) có đúng hai nghiệm phân biệt t > 0 ⇔ đường thẳng y cắt đồng thời hai parabol tại đúng hai điểm có hoành độ dương
tại đúng hai điểm có hoành độ dương 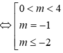

Vậy có tất cả 23 số nguyên thoả mãn yêu cầu bài toán.
Chọn đáp án B.