Trong không gian Oxyz cho cho hai mặt phẳng : 3x-2y+3z+5=0 và : 9x-6y-9z-5=0. Tìm khẳng định đúng.
A. và trùng nhau
B. và song song
C. và vuông góc
D. và cắt nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có
α : x − 2 y + 3 z − a = 0 ⇔ 3 x − 6 y + 9 z − 3 a = 0.
Gọi h là chiều cao của hình lăng trụ, do α / / β nên h = d α ; β = b + 3 a 3 14 .
Ta có
V = S . h ⇔ 5 14 = 5. b + 3 a 3 14 = 3 a + b = 42 ⇔ a + b 3 = 14

Chọn đáp án C
Mặt phẳng (P) có vectơ pháp tuyến là n 1 ⇀ = 2 ; a ; 3 ; mặt phẳng (Q) có vectơ pháp tuyến là n 2 ⇀ = b ; - 6 ; - 6 .
Để (P)//(Q) thì n 1 ⇀ , n 2 ⇀ cùng phương hay n 1 ⇀ = k n 2 ⇀
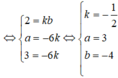

\(\left\{{}\begin{matrix}x=4+2t\\y=1-5t\end{matrix}\right.\)
Vậy: VTCP là (2;-5) và điểm mà (d1) đi qua là A(4;1)
=>VTPT là (5;2)
Phương trình đường thẳng của (d1) là:
5(x-4)+2(y-1)=0
=>5x-20+2y-2=0
=>5x+2y-22=0
(d2): 2x-5y-14=0
=>(d1) và (d2) vuông góc

Đáp án B.
Để α / / β thì 2 1 = 4 2 = − m − 1 ≠ − 2 − 1 ⇒ không tồn tại m.
Đáp án D