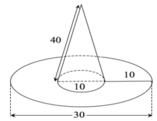
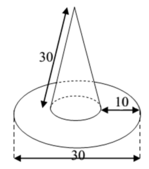
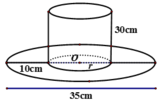
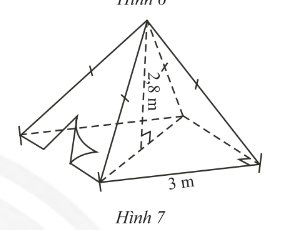
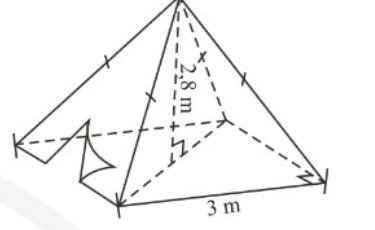
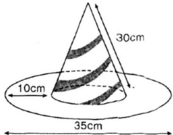
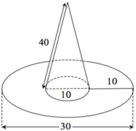
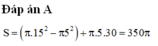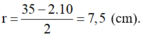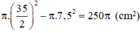Tính diện tích vải tối thiểu để may được một chiếc mũ có hình dạng và kích thước (cùng đơn vị đo) được cho bởi hình vẽ bên (không kể viền, mép) biết phía trên có dạng một hình nón và phía dưới (vành mũ) có dạng hình vành khăn.
A. 450π.
B. 500π.
C. 350π.
D. 400π.