Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Một khu đồi trồng cây ăn quả có tất cả 1950 cây, gồm các loại cam, quýt và vải thiều. Biết \(\dfrac{2}{3}\) số cây cam bằng \(\dfrac{3}{5}\) cây quýt và bằng \(\dfrac{6}{7}\) số cây vải thiều. Tính xem mỗi loại có bao nhiêu cây.
\(\dfrac{2}{3}\) số cây cam bằng \(\dfrac{3}{5}\) cây quýt và bằng \(\dfrac{6}{7}\) số cây \(\Rightarrow\) \(\dfrac{6}{9}\) số cây cam bằng \(\dfrac{6}{10}\) cây quýt và bằng \(\dfrac{6}{7}\) số cây vải thiều
Ta có sơ đồ:
Cam |-------|-------|-------|-------|-------|-------|-------|-------|-------| (9 phần)
Quýt |-------|-------|-------|-------|-------|-------|-------|-------|-------|-------| (10 phần)
Vải |-------|-------|-------|-------|-------|-------|-------| (7 phần)
Số cây cam là:
\(1950:\left(9+10+7\right).9=675\) (cây)
Số cây quýt là:
\(1950:\left(9+10+7\right).10=750\) (cây)
Số cây vải thiều là:
\(1950:\left(9+10+7\right).7=525\) (cây)
Đáp số: Quýt: 675 cây
Quýt: 750 cây
Vải: 525 cây
2. Một mảnh đất được chia thành 3 phần. Phần để xây nhà có diện tích chiếm \(\dfrac{3}{5}\) diện tích mảnh đất. Phần để làm sân có diện tích bằng 24% diện tích mảnh đất, phần diện tích còn lại là 24m2 để trồng cây cảnh.
a) Tính diện tích mảnh đất
Phân số chỉ phần diện tích còn lại để trồng cây cảnh là:
\(1-\dfrac{3}{5}-24\%=\dfrac{4}{25}\) (tổng số đất)
Diện tích mảnh đất là:
\(24:\dfrac{4}{25}=150m^2 \)
b) Tính diện tích phần đất để làm nhà
Diện tích phần đất để làm nhà là:
\(150.\dfrac{3}{5}=90m^2\)
Đáp số: a) \(150m^2\)
b) \(90m^2\)

Phần diện tích trồng cây cảnh chiếm
1-3/5-24%=4/25 ( diện ích mảnh đất)
* Diện tích mảnh đất là:
24:4/25=150 ( m2)
Diện tích đất để làm nhà là:
150.3/5=90 ( m2)
Đáp số: Diện tích mảnh đất: 150 m2
Diện tích làm nhà: 90 m2

a+3c=8 nên c=(8-a)/3
a+2b=9 nên b=(9-a)/2
=>a+3c+a+2b=8+9
2a+2b+2c+c=17
2(a+b+c)=17+c
2[a+(9-a)/2+(8-a)/3]=17+(8-a)/3
2[6a/6+(27-3a)/6+(16-2a)/6]=17+(8-a)/3
2[(6a+27-3a+16-2a)/6]=17+(8-a)/3
2*(a+43)/6=17+(8-a)/3
(a+43)/3-(8-a)/3=17
(a+43-8+a)/3=17
2a+35=17*3=51
2a=51-35
2a=16
a=16/2
a=8
t k chắc, tính nhẩm k cầm mt
Ta có:
a+3c=8 (1)
a+2b=9 (2)
Cộng từng vế các BĐT (1);(2)
=>a+3c+a+2b=8+9
=>(a+a)+3c+2b=17
=>2a+2c+c+2b=17
=>2a+2c+2b+c=17
=>2(a+b+c)+c=17
a+b+c lớn nhất <=>c nhỏ nhất
Mà c >= 0 (do c không âm)
=>c=0
Thay c=0 vào (1) ta có:a+3.0=8=>a+0=8=>a=8
Vậy a=8 thỏa mãn
(*)Linh ak,c từng nói t là super làm dài,bài này thì c cũng đâu khác t đâu? ![]()


Đáp án D
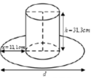
Diện tích S 1 là S 1 = 2 π r h + π r 2 = 62 , 6 π r + π r 2 ( diện tích toàn phần trừ một đáy)
Diện tích S 2 là S 2 = π 11 , 1 + r 2 − π r 2 = π 123 , 21 + 22 , 2 r ( diện tích hình tròn to trừ hình tròn nhỏ)
Khi đó:
P = 3 S 2 − S 1 = 3 π 22 , 2 r + 123 , 21 − 62 , 6 π r − π r 2 = 369 , 63 π + 4 π r − π r 2
Ta có:
4 r − r 2 = 4 − 2 − r 2 ≤ 4 ⇔ π 4 r − r 2 ≤ 4 π ⇒ P ≤ 373 , 63 π
Dấu “=” xảy ra khi và chỉ khi:
r = 2 ⇒ d = 2 x + r = 2 11 , 1 + 2 = 26 , 2 ⇒ r + d = 28 , 2