Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số C : y = m x − x 2 − 2 x + 2 có tiệm cận ngang?
A. 2
B. 3
C. 1
D. 4.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 4 2018
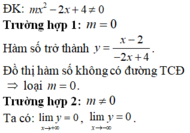
Suy ra đồ thị hàm số có 1 đường TCN y = 0.
Do đó đồ thị hàm số có đúng 2 đường tiệm cận đồ thị hàm số có đứng 1 đường tiệm cận đứng phương trình m x 2 - 2 x + 4 = 0 có nghiệm kép hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm x = 2.
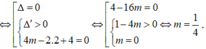
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
Với \(m=0\) ko thỏa mãn
Với \(m\ne0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=-\dfrac{1}{\sqrt{m}}\); \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) Hàm có 2 TCN khi \(\sqrt{m}\) xác định \(\Rightarrow m>0\)
CM
5 tháng 1 2020
Ta có 
đồ thị hàm số luôn có TCN y = 1
Do đó để ycbt thỏa mãn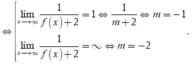 
Chọn C.
CM
13 tháng 7 2019
Chọn C
Ta có:
nên đồ thị hàm số luôn có 1 TCN là y = 0
Đồ thị hàm số có 2 đường tiệm cận thì nó chỉ có duy nhất 1 đường tiệm cận đứng
⇔ phương trình x 2 + m x + 4 = 0 có nghiệm x = 1
hoặc phương trình x 2 + m x + 4 = 0 có nghiệm kép (có thể bằng 1)
Vậy có 3 giá trị của m thỏa mãn bài toán
CM
1 tháng 8 2019
Đáp án B
Phương pháp:
Đồ thị của hàm số y = f(x) có hai tiệm cận ngang ó Tập xác định của y = f(x) chứa khoảng âm vô cực và dương vô cực và
∃
a,b
∈
R, a
≠
b: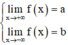 
Cách giải: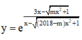 
Điều kiện xác định: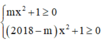 
Đồ thị hàm số 
có 2 tiệm cận ngang => Tập xác định D phải chứa khoảng âm vô cực và dương vô cực
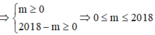
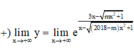
Ta tìm m để tồn tại giá trị của a ∈ R
TH1: 
. Khi đó 
R
TH2: 
. Khi đó 
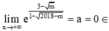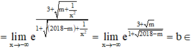R
R, 
+) Giải phương trình:
Vậy, với mọi số nguyên 
hàm số 
luôn có 2 tiệm cận ngang.
Số giá trị nguyên của m thỏa mãn là: 2019 số.
CM
1 tháng 1 2017
Điều kiện: mx2+ 1 > 0.
- Nếu m= 0 thì hàm số trở thành y= x+ 1 không có tiệm cận ngang.
- Nếu m< 0 thì hàm số xác định ⇔ - 1 - m < x < 1 - m
Do đó, lim x → ± ∞ y không tồn tại nên đồ thị hàm số không có tiệm cận ngang.
- Nếu m> 0 thì hàm số xác định với mọi x.
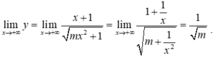
Suy ra đường thẳng y = 1 m là tiệm cận ngang của đồ thị hàm số khi x → + ∞ .
Suy ra đường thẳng y = - 1 m là tiệm cận ngang của đồ thị hàm số khi x → - ∞
Vậy m> 0 thỏa mãn yêu cầu đề bài.
Chọn D.
11 tháng 1
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m+3\right)x-5}{x+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m+3\right)x-5}{x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
=>Đường thẳng y=2m+3 là đường tiệm cận ngang duy nhất của đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\)
Để đường thẳng y=2m+3 đi qua A(-1;3) thì 2m+3=3
=>2m=0
=>m=0
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
=>Đường thẳng \(y=m^2-3m\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
=>\(m^2-3m=-2\)
=>\(m^2-3m+2=0\)
=>(m-1)(m-2)=0
=>m=1 hoặc m=2
Đáp án A
Đường thẳng y = y 0 được gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f x nếu lim x → + ∞ f x = y 0 hoặc lim x → − ∞ f x = y 0
y = m x − x 2 − 2 x + 2 = m 2 x 2 − x 2 + 2 x − 2 m x + x 2 − 2 x + 2 = m 2 − 1 x 2 + 2 x − 2 m x + x 2 − 2 x + 2
Để hàm phân thức có tiệm cận ngang thì bậc tử phải nhỏ hơn hoặc bằng bậc mẫu ⇔ m 2 − 1 = 0 ⇔ m = 1 m = − 1
Vậy có 2 giá trị của m thỏa mãn yêu cầu bài toán.