Cho khối chóp tam giác SABC có AB=AC=a, ∠ B A C = 120 ° , ∠ S B A = S C A = 90 ° . Góc giữa SB và mặt phẳng (ABC) bằng 60 ° . Thể tích khối chóp S.ABC bằng
A. a 3 4
B. 3 a 3 4
C. a 3 2
D. 3 a 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
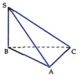
Ta có S B ⊥ ( A B C ) ⇒ B C là hình chiếu của SC trên mặt phẳng (ABC).
Suy ra S C , ( A B C ) ^ = S C , B C ^ = S C B ^ = 60 0
Do Δ A B C vuông tại A nên
S B = B C . tan S C B ^ = 2 a . tan 60 0 = 2 a 3 .
⇒ B C = A B 2 + A C 2 = a 2 + a 3 2 = 2 a .
Do Δ S B C vuông tại B nên
S B = B C . tan S C B ^ = 2 a . tan 60 0 = 2 a 3 .
Vậy
V S . A B C = 1 3 S B . S Δ A B C = 1 6 S B . A B . A C = 1 6 .2. 3 a . a . a 3 = a 3 (đvtt).

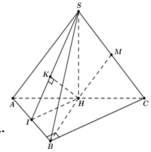
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.
Hạ S D ⊥ ( A B C ) Ta có:
⇒ B A ⊥ D B ⇒ ∠ D B C = 60 ° Tương tự ta có
⇒ C A ⊥ D C ⇒ ∠ C D B = 60 °
Do đó ∆ C B D đều cạnh
Vậy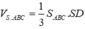
Chọn đáp án B.