Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trong mặt phẳng (ABCD) gọi AC giao BD tại I
Một điểm chung của hai mặt phẳng (SAC) và (SBD) khác điểm S là điểm I
I ∈ AC ⊂ (SAC)
I ∈ BD ⊂ (SBD)
Đáp án B
Ta có: NI ∩ SD = J
Xét (CMN) và (SAD) có:
M là điểm chung
J là điểm chung
⇒ MJ là giao tuyến của 2 mặt phẳng (CMN) và (SAD)
\(\left\{{}\begin{matrix}S=\left(SAC\right)\cap\left(SBD\right)\\O=\left(SAC\right)\cap\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b.
Trong mp (SAC), nối MO kéo dài cắt SC kéo dài tại H
\(\left\{{}\begin{matrix}H\in MO\\H\in SC\in\left(SCD\right)\end{matrix}\right.\) \(\Rightarrow H=MO\cap\left(SCD\right)\)
Đáp án C
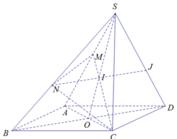
Trong (SAC) có SO cắt MC tại I
I ∈ MC ⇒ I ∈ (MNC)
Mà I ∈ SO
⇒ I là giao điểm của SO và (MNC)
\(AC\in P;BD\in P\) => AC căt BD tại I
\(AC\in\left(SAC\right)\Rightarrow I\in\left(SAC\right)\)
\(BD\in\left(SBD\right)\Rightarrow I\in\left(SBD\right)\)
=> I là điểm chung của (SAC) và (SBD)