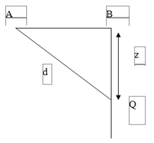
Trên mặt thoáng của một chất lỏng có hai nguồn A, B cách nhau 3cm dao động cùng phương, ngược pha, phát ra hai sóng kết hợp với bước sóng 1cm. Gọi Q là một điểm nằm trên đường thẳng qua B, vuông góc với AB cách B một đoạn z. Để Q dao động với biên độ cực đại thì z có giá trị lớn nhất và nhỏ nhất lần lượt là
A. 4cm và 0,55cm
B. 4cm và 1,25cm
C. 8,75cm và 1,25cm
D. 8,75cm và 0,55cm

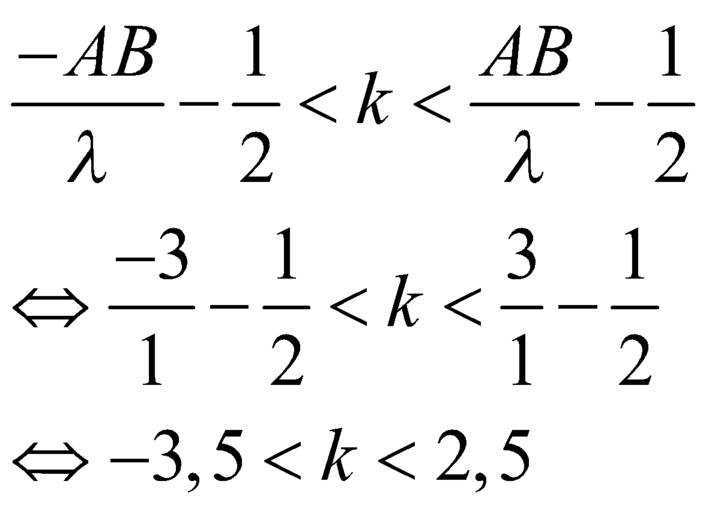
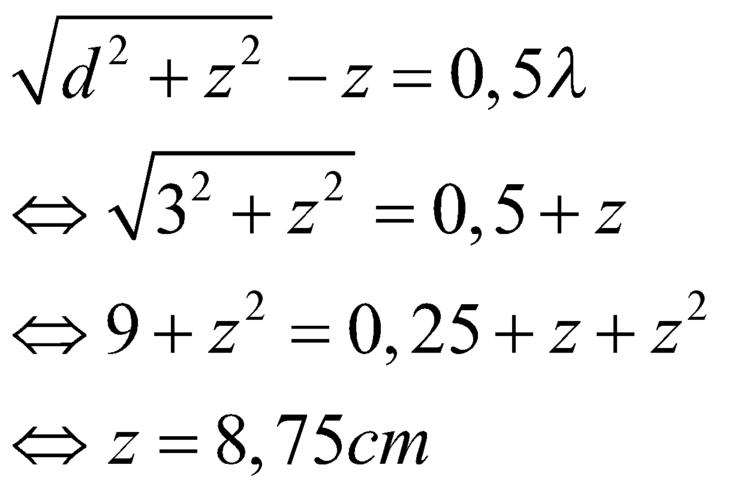
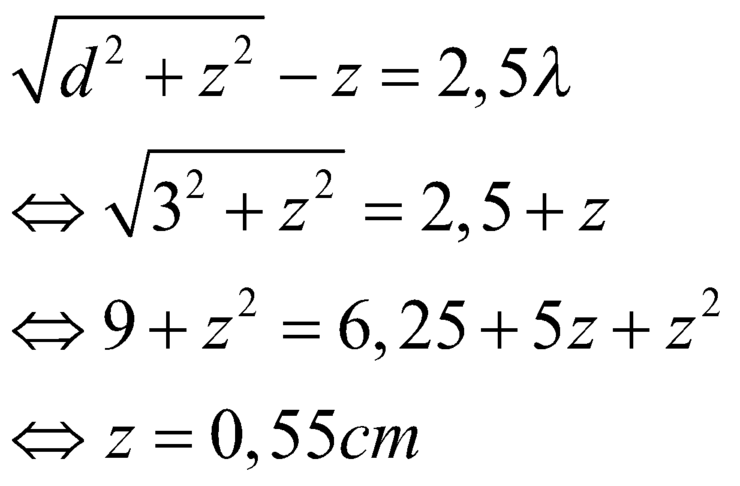




Đáp án D
Ta có hình vẽ
Vì hai nguồn dao động ngược pha nên ta áp dụng điều kiện để 1 điểm trong miền giao thoa dao động cực đại là:
d 1 - d 2 = ( k + 1 2 ) λ
Suy ra, điểm Q dao động cực đại khi:
d 2 + z 2 - z = ( k + 1 2 ) λ
Vì Q dao động cực đại nên điểm Q nằm trên các đường hyperbol cực đại trong miền giao thoa.
Áp dụng công thức tính số dao động cực đại trong đoạn AB:
- AB λ - 1 2 < k < AB λ - 1 2 ⇔ - 3 1 - 1 2 < k < 3 1 - 1 2
⇔ - 3 , 5 < k < 2 , 5
Vậy k nhận các giá trị : -3; +-2; +- 1; 0
Từ điều kiện Q dao động cực đại, khi Q xa nhất ứng với k = 0, thay số vào ta được:
d 2 + z 2 - z = 0 , 5 λ ⇔ 3 2 + z 2 = 0 , 5 + z
⇔ 9 + z 2 = 0 , 25 + z + z 2 ⇔ z = 8 , 75 cm .
Khi Q gần nhất ứng với k = 2 (hoặc k = -3, tùy theo bạn chọn đâu là chiều dương), thay số vào ta được:
d 2 + z 2 - z = 2 , 5 λ ⇔ 3 2 + z 2 = 2 , 5 + z
⇔ 9 + z 2 = 6 , 25 + 5 z + z 2 ⇔ z = 8 , 75
Vậy Zmin =0,55cm; Zmax = 8,75cm.