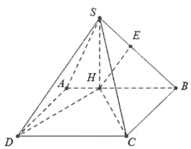
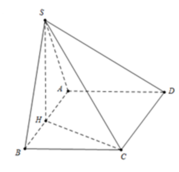
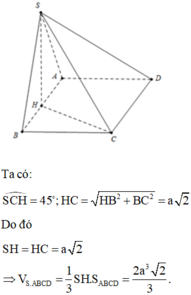
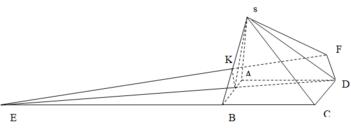
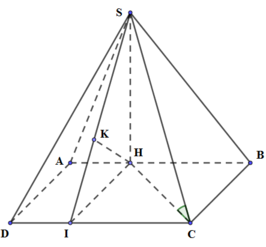
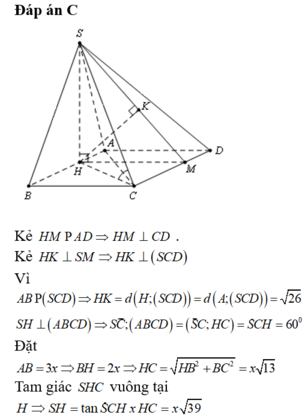
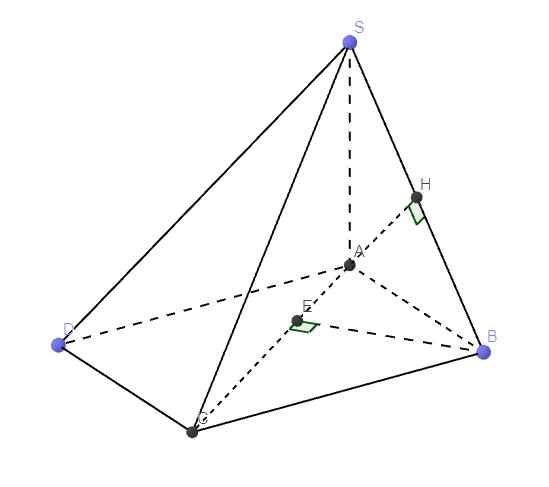
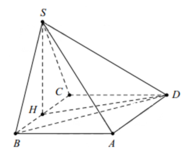
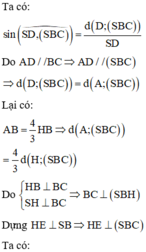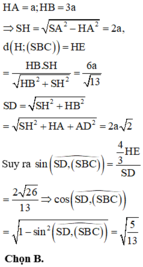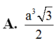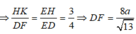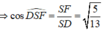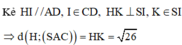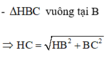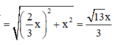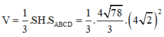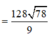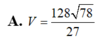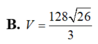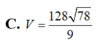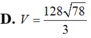Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, S A = a 5 , A B = 4 a , A D = a 3 . Điểm H nằm trên cạnh AB thỏa mãn A H = 1 3 H B , hai mặt phẳng (SHC) và (SHD) cùng vuông góc với mặt phẳng đáy. Cosin góc giữa SD và (SBC) bằng
A. 5 12
B. 5 13
C. 4 13
D. 3 3