Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
E=AB∩CD,G=EN∩SB⇒GE=AB∩CD,G=EN∩SB⇒G là trọng tâm tam giác SAE.
d(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
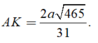

a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
c: (SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=căn 3
=>góc SCA=60 độ

Đáp án C
Kẻ CN
⊥
AB ta dễ dàng tính được ![]()
![]()
=> tam giác ADC vuông tại C. Từ đó NC ⊥ (SAC)
Gọi O là trung điểm của AC, dễ dàng cm được BD ⊥ (SAC)
=> MK ⊥ (SAC). vơí K là trung điểm của SO, từ đó KC là hc của MN lên .
Ta kẻ KZ ⊥ AC
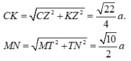
với T là trung điểm của AB.
Gọi α là góc tạo với MN và (SAC)
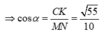

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)

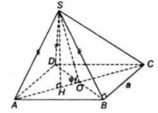
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
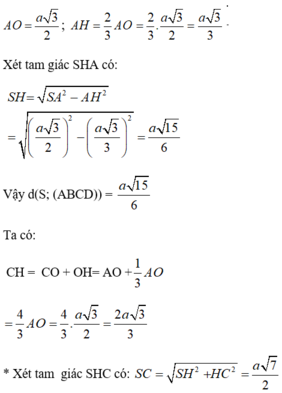

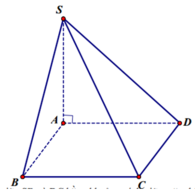

Ta có:
\(\left\{{}\begin{matrix}BH\cap\left(SAC\right)=S\\BS=2HS\end{matrix}\right.\) \(\Rightarrow d\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(B;\left(SAC\right)\right)\)
Từ B kẻ \(BE\perp AC\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BE\\BE\perp AC\end{matrix}\right.\) \(\Rightarrow BE\perp\left(SAC\right)\)
\(\Rightarrow BE=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BE^2}=\dfrac{1}{AB^2}+\dfrac{1}{BC^2}=\dfrac{3}{2a^2}\Rightarrow BE=\dfrac{a\sqrt{6}}{3}\)
\(\Rightarrow h\left(H;\left(SAC\right)\right)=\dfrac{1}{2}BE=\dfrac{a\sqrt{6}}{6}\)
b.
Ta có: \(CD||AB\Rightarrow CD||\left(SAB\right)\)
Mà \(AH\in\left(SAB\right)\Rightarrow d\left(AH,CD\right)=d\left(CD;\left(SAB\right)\right)=d\left(D;\left(SAB\right)\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD=d\left(D;\left(SAB\right)\right)\)
\(\Rightarrow d\left(AH;CD\right)=AD=a\sqrt{2}\)