Cho x > 0, x ≠ 1 thỏa mãn biểu thức 1 log 2 x + 1 log 3 x + . . . + 1 log 2017 x = M. Chọn khẳng định đúng trong các khẳng định sau:
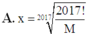
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có log(x + 2y) = log x + log y
<=> log 2 (x+2y) = log 2xy
<=> 2 (x+2y) = 2xy (*).
Đ ặ t a = x > 0 b = 2 y > 0 , khi đó
* ⇔ 2 a + b = a b
và P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2
Lại có a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8 .
Đặt t = a + b, do đó
P ≥ f t = t 2 t + 2 .
X é t h à m s ố f t = t 2 t + 2 t r ê n [ 8 ; + ∞ )
c ó f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ ≥ 8
Suy ra f(t) là hàm số đồng biến trên [ 8 ; + ∞ )
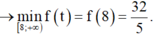
Vậy gía trị nhỏ nhất của biểu thức P là 32 5 .

\(A=log_2\left(x^3-x\right)-log_2\left(x+1\right)-log_2\left(x-1\right)\)
\(=log_2\left(\dfrac{x^3-x}{x+1}\right)-log_2\left(x-1\right)\)
\(=log_2\left(\dfrac{x\left(x-1\right)\left(x+1\right)}{x+1}\right)-log_2\left(x-1\right)\)
\(=log_2\left(\dfrac{x\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\right)=log_2x\)

a)
ĐK: \(\left\{{}\begin{matrix}2x-4>0\\x-1>0\end{matrix}\right.\Leftrightarrow x>1\)
\(\log_5\left(2x-4\right)+\log_{\dfrac{1}{5}}\left(x-1\right)=0\\ \Leftrightarrow\log_5\left(2x-4\right)-\log_5\left(x-1\right)=0\\ \Leftrightarrow\log_5\left(\dfrac{2x-4}{x-1}\right)=\log_51\\ \Leftrightarrow\dfrac{2x-4}{x-1}=1\\ \Leftrightarrow2x-4=x-1\\ \Leftrightarrow x=3\left(tm\right)\)
Vậy x = 3.
b) ĐK: x > 0
\(\log_2x+\log_4x=3\\ \Leftrightarrow\log_2x+\dfrac{1}{2}\log_2x=3\\ \Leftrightarrow\left(1+\dfrac{1}{2}\right)\log_2x=3\\ \Leftrightarrow\dfrac{3}{2}\log_2x=3\\ \Leftrightarrow\log_2x=2\\ \Leftrightarrow x=4\left(tm\right)\)
Vậy x= 4

a)
Điều kiện để $1-2x > 0$ (đối số dương) là:
$1 > 2x$
$x < \frac{1}{2}$
Vậy, để biểu thức $log_3(1-2x)$ có nghĩa, giá trị của $x$ phải nhỏ hơn $\frac{1}{2}$.

a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)
Với \(x = 2\) thì \(y = {\log _2}2 = 1\)
Với \(x = 4\) thì \(y = {\log _2}4 = 2\)
b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.

Theo đầu bài ta có: log 2x+ log2y=log4(x+y) hay 2 log 2(xy) =log2(x+y)
Suy ra x+y=(xy) 2
Đặt u= x+ y; v= xy ta có điều kiện u2-4v≥0; u>0; v>0 .
Mà ![]()
Ta có
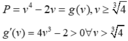
nên minP=
2
4
3
khi 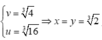
Chọn A.

a) \({3^{{x^2} - 4x + 5}} = 9 \Leftrightarrow {x^2} - 4x + 5 = 2 \Leftrightarrow {x^2} - 4x + 3 = 0 \Leftrightarrow \left( {x - 3} \right)\left( {x - 1} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Vậy phương trình có nghiệm là \(x \in \left\{ {1;3} \right\}\)
b) \(0,{5^{2x - 4}} = 4 \Leftrightarrow 2x - 4 = {\log _{0,5}}4 \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\)
Vậy phương trình có nghiệm là x = 1
c) \({\log _3}(2x - 1) = 3\) ĐK: \(2x - 1 > 0 \Leftrightarrow x > \frac{1}{2}\)
\( \Leftrightarrow 2x - 1 = 27 \Leftrightarrow x = 14\) (TMĐK)
Vậy phương trình có nghiệm là x = 14
d) \(\log x + \log (x - 3) = 1\) ĐK: \(x - 3 > 0 \Leftrightarrow x > 3\)
\(\begin{array}{l} \Leftrightarrow \log \left( {x.\left( {x - 3} \right)} \right) = 1\\ \Leftrightarrow {x^2} - 3x = 10\\ \Leftrightarrow {x^2} - 3x - 10 = 0\\ \Leftrightarrow \left( {x + 2} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2 (loại) \,\,\,\\x = 5 (TMĐK) \,\,\,\,\,\,\,\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm x = 5
Đáp án D