Cho hình chóp S.ABC có SA = 2a, SB = 3a và ∠ ASB = ∠ BSC = 60 0 , ∠ ASC = 90 0 . Tính thể tích V của khối chóp S.ABC
c
B. V = 4 a 3 2 3
C. V = 2 a 3 2
D. V = 2 a 3 2 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Gọi M là điểm trên đoạn SC sao cho SC=3SM Tính được AB=BM=a, A M = a 2 =>DABM vuông tại B, suy ra trung điểm H của AM là tâm đường tròn ngoại tiếp DABM. Suy ra
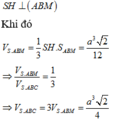

Chọn A
Trên cạnh SB, SC lần lượt lấy các điểm M, N thỏa mãn SM = SN = 1.
Ta có AM = 1, AN = 2 , MN = 3
=> tam giác AMN vuông tại A
Hình chóp S.AMN có SA = SM = SN = 1.
=> hình chiếu của S trên (AMN) là tâm I của đường tròn ngoại tiếp tam giác AMN, ta có I là trung điểm của MN
Trong
∆
SIM, 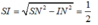
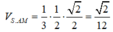
Ta có 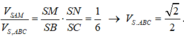
Phương pháp:
+) Lấy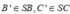 sao cho SA = SB' = SC' = 2a. Chóp có các cạnh bên bằng nhau có chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.
sao cho SA = SB' = SC' = 2a. Chóp có các cạnh bên bằng nhau có chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.
+) Tính thể tích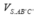
Cách giải:
Lấy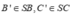 sao cho SA = SB' = SC' = 2a.
sao cho SA = SB' = SC' = 2a.
=> AB' = B'C' = 2a
Xét tam giác vuông SAC' có: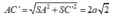
Xét tam giác AB'C' có: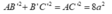
Do đó tam giác AB'C' vuông tại B' (Định lí Pytago đảo).
Gọi H là trung điểm của AC' => H là tâm đường tròn ngoại tiếp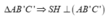
Ta có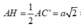
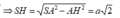
Chọn: C