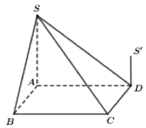
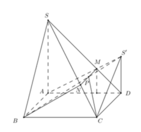
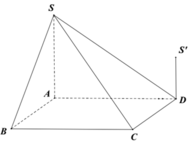
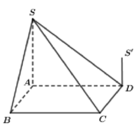
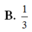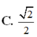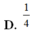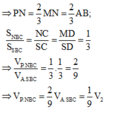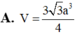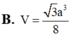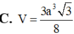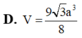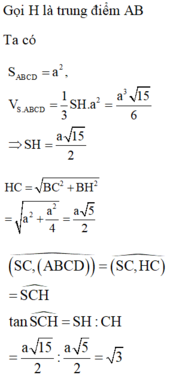Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Trên đường thẳng vuông góc với tại D lấy điểm S’ thỏa mãn S ' D = 1 2 S A và S, S’ ở cùng phía đối với mặt phẳng (ABCD). Gọi V 1 là thể tích phần chung của hai khối chóp S.ABCD và S’.ABCD. Gọi V 2 là thể tích khối chóp S.ABCD, tỉ số V 1 V 2 bằng
![]()