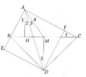
CHO TAM GIÁC ABC VÔNG TẠI A, TRUNG TUYẾN AM. LẤY N ĐỐI XỨNG VỚI A QUA M
a, TỨ GIÁC ACNB LÀ HÌNH GÌ?
b, QUA A KẺ ĐƯỜNG THẲNG d // BC
LẤY Q THUỘC d ( Q THUỘC NỬA MẶT PHẲNG BỜ AN KHÔNG CHỨA B) SAO CHO AD=BC
CM Q VÀ N ĐỐI XỨNG VỚI NHAU QUA CHO TAM GIÁC ABC VÔNG TẠI A, TRUNG TUYẾN AM. LẤY N ĐỐI XỨNG VỚI A QUA M
a, TỨ GIÁC ACNB LÀ HÌNH GÌ?
b, QUA A KẺ ĐƯỜNG THẲNG d // BC
LẤY Q THUỘC d ( Q THUỘC NỬA MẶT PHẲNG BỜ AN KHÔNG CHỨA B) SAO CHO AD=BC
CM Q VÀ N ĐỐI XỨNG VỚI NHAU QUA C