Cho hình lập phương A B C D . A ' B ' C ' D ' có đường chéo bằng a 3 . Tính thể tích khối chóp A ' A B C D ?
A. a 3 3
B. 2 a 3 2 3
C. a 3
D. 2 a 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
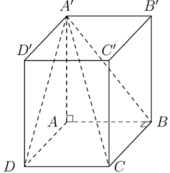
Ta có: hình lập phương ABCD.A'B'C'D' có đường chéo bằng a 3
Suy ra cạnh của hình lập phương bằng a.
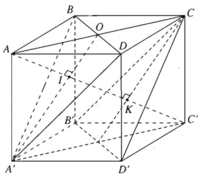
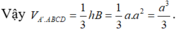 Vậy
V
A
'
.
A
B
C
D
=
1
3
h
B
=
1
3
a
.
a
2
=
a
3
3
Vậy
V
A
'
.
A
B
C
D
=
1
3
h
B
=
1
3
a
.
a
2
=
a
3
3

Chọn B.
Hình nón A.A'BCD' với đáy là hình chữ nhật A'BCD' có diện tích S = A'B.BC = a 2 √2 và chiều cao h = (a 2 )/2 nên có thể tích V = a 3 /3

\(AC=AB\sqrt{2}=4a\)
Áp dụng định lý Pitago:
\(CC'=\sqrt{\left(AC'\right)^2-AC^2}=3a\)
\(\Rightarrow V=3a.\left(2a\sqrt{2}\right)^2=24a^3\)

Điểm A cách đều ba đỉnh của tam giác đều A'BD vì ta có AB = AD = AA′ = a, điểm C' cũng cách đều ba đỉnh của tam giác đều đó vì ta có:
C′B = C′D = C′A′ = a√2
Vậy AC' là trục của đường tròn ngoại tiếp tam giác A'BD, tức là đường thẳng AC' vuông góc với mặt phẳng (A'BD) tại trọng tâm I của tam giác A'BD. Ta cần tìm khoảng cách A'I.
Ta có A′I = BI = DI = 2A′O/3 với O là tâm của hình vuông ABCD
Ta lại có 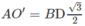
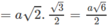
Vậy 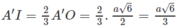
Tương tự điểm C' cách đều ba đỉnh của tam giác đều CB'D', tính được khoảng cách từ C, B', D' tới đường chéo AC'.