Tính tích phân I = ∫ 0 π 2 cos 4 x sin x d x , bằng cách đặt t=cosx, mệnh đề nào đưới đây đúng?
A. I = ∫ 0 1 t 4 d t
B. I = - ∫ 0 1 t 4 d t
C. I = ∫ 0 π 2 t 4 d t
D. I = - ∫ 0 π 2 t 4 d t
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

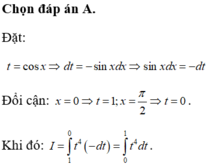

Đáp án B
Đặt x = 2 sin t , t ∈ − π 2 ; π 2 ⇒ d x = 2 cos t d t . Đổi cận x = 0 ⇒ t = 0 x = 1 ⇒ t = π 6
Suy ra I = ∫ 0 π 6 2 4 − 4 sin 2 t .2 cos t d t = 2 ∫ 0 π 6 d t

\(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2xdx\\v=\dfrac{1}{2}sin2x\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{2}x^2sin2x|^{\pi}_0-\int\limits^{\pi}_0x.sin2xdx\)

Đáp án A.
u = x 2 d v = c o s 2 x d x ⇒ d u = 2 x d x v = 1 2 sin 2 x ⇒ I = 1 2 x 2 sin 2 x π 0 − ∫ 0 π x sin 2 x d x .