Hai nguồn kết hợp A, Β trên mặt nước cách nhau một đoạn AB = 7λ (λ là bước sóng) dao động với phương trình u A = u B = cosωt. Trên đoạn AB, số điểm có biên độ cực đại và ngược pha với hai nguồn (không kể hai nguồn) là
A. 8.
B. 7.
C. 10.
D. 14.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
+ Điểm M thuộc đoạn AB có phương trình: u M = 2 a cos π d 2 - d 1 λ cos ω t - 7 π ( * )
M có biên độ cực đại và cùng pha với nguồn:
⇒ d 2 - d 1 = ( 2 k + 1 ) λ
+ Mặc khác M ∈ AB => d 2 + d 1 = A B = 7 λ ( 1 )
và (2) ⇒ d 2 = k λ + 4 λ < 7 λ ⇒ -4<k<3
+ Vậy: k = -3;-2;-1;0;1;2 => có 6 giá trị k

Đáp án B
Điểm M thuộc đoạn AB có phương trình:
![]() (*)
(*)
M có biên độ cực đại và cùng pha với nguồn:![]()
Mặc khác ![]() (1)
(1)
và (2) 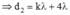 với
với ![]()
→ ![]()
Vậy: ![]() Có 6 giá trị của k
Có 6 giá trị của k

Đáp án C
Gọi M là điểm trên AB cách A và B lần lượt d1 và d2.
Ta có: d1 + d2 = AB = 7λ. Sóng tại M do từ A và B truyền đến có phương trình lần lượt là:


Đáp án A
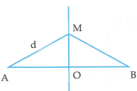
Biểu thức sóng tại A, B:
u
=
a
cos
ω
t
. Xét điểm M nằm trên đường trung trực của AB:
A
M
=
B
M
=
d
c
m
≥
10
c
m
. Biểu thức sóng tại M là:
u
M
=
2
a
cos
ω
t
-
2
πd
λ
. Điểm M dao động cùng pha với nguồn khi: ![]() nên
nên ![]()

Đáp án B
Phương pháp: Viết phương trình dao động của phần tử tại M, xét đặc điểm của pha và biên độ.
Cách giải:
Đặt phương trình dao động tại hai nguồn là: u A = u B = a cos ω t
Ta có phương trình dao động của phần tử môi trường tại M là:
u M = 2 . a . cos ( π ( d 2 - d 1 ) λ . cos ( ω t - π ( d 2 + d 1 ) λ
Do M nằm trên AB nên d2 + d1 =AB = 13λ, Thay vào phương trình ta được :
u M = 2 . a . cos ( π ( d 2 - d 1 ) λ ) . cos ( ω t - 13 π )
Vậy phần tử tại M luôn dao động ngược pha so với nguồn, cần tìm điều kiện để M cực đại:
π ( d 2 - d 1 ) λ = k 2 π ⇒ d 2 - d 1 = k 2 λ
Áp dụng điêu kiện:
- A B ≤ d 2 - d 1 ≤ A B ⇔ - 13 λ ≤ 2 k λ ≤ 13 λ ⇔ - 13 ≤ 2 k ≤ 13 ⇔ - 6 , 5 ≤ ≤ 6 , 5
Các giá trị k thỏa mãn là : k = 0; ±1; ±2…±6
Vậy có 13 điểm.