Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi M là điểm trên AB cách A và B lần lượt d1 và d2.
Ta có: d1 + d2 = AB = 7λ. Sóng tại M do từ A và B truyền đến có phương trình lần lượt là:


Đáp án B
Phương pháp: Viết phương trình dao động của phần tử tại M, xét đặc điểm của pha và biên độ.
Cách giải:
Đặt phương trình dao động tại hai nguồn là: u A = u B = a cos ω t
Ta có phương trình dao động của phần tử môi trường tại M là:
u M = 2 . a . cos ( π ( d 2 - d 1 ) λ . cos ( ω t - π ( d 2 + d 1 ) λ
Do M nằm trên AB nên d2 + d1 =AB = 13λ, Thay vào phương trình ta được :
u M = 2 . a . cos ( π ( d 2 - d 1 ) λ ) . cos ( ω t - 13 π )
Vậy phần tử tại M luôn dao động ngược pha so với nguồn, cần tìm điều kiện để M cực đại:
π ( d 2 - d 1 ) λ = k 2 π ⇒ d 2 - d 1 = k 2 λ
Áp dụng điêu kiện:
- A B ≤ d 2 - d 1 ≤ A B ⇔ - 13 λ ≤ 2 k λ ≤ 13 λ ⇔ - 13 ≤ 2 k ≤ 13 ⇔ - 6 , 5 ≤ ≤ 6 , 5
Các giá trị k thỏa mãn là : k = 0; ±1; ±2…±6
Vậy có 13 điểm.

Chọn đáp án B
I năm trên trung trực của AB =>> IOA vuông tai O.mà I cùng pha với A,B =>> IA=IB=kλ =8k I gần o nhất.mà OA=10 =>> k=2 tm =>> IA=16 =>> IO^2=IA^2-OA^2=16^2-10^2=156 => IO=căn 156 =>> B đúng

- Gọi d1, d2 là khoảng cách từ M đến 2 nguồn (M thuộc đường tròn và thỏa yêu cầu)
+ M thuộc đường tròn nên góc AMB là góc vuông
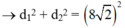
+ M dao động với biên độ cực đại nên: d1 - d2 = kλ
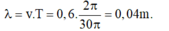
- Giải hệ phương trình trên ta được:
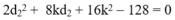
+ Chỉ có k = 0 là thỏa mãn ⇒ d1 = d2 = 8 cm
+ M dao động cùng pha với nguồn nên:
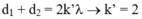
- Vậy có tất cả 2 điểm.


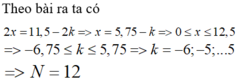

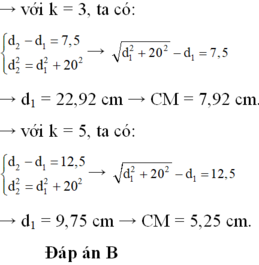

Chọn B
+ Điểm M thuộc đoạn AB có phương trình: u M = 2 a cos π d 2 - d 1 λ cos ω t - 7 π ( * )
M có biên độ cực đại và cùng pha với nguồn:
⇒ d 2 - d 1 = ( 2 k + 1 ) λ
+ Mặc khác M ∈ AB => d 2 + d 1 = A B = 7 λ ( 1 )
và (2) ⇒ d 2 = k λ + 4 λ < 7 λ ⇒ -4<k<3
+ Vậy: k = -3;-2;-1;0;1;2 => có 6 giá trị k