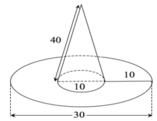
Tính diện tích vải tối thiểu để may được chiếc mũ có hình dạng và kích thước (cùng đơn vị đo) được cho bởi hình vẽ bên (không kể viền, mép) biết phía trên có dạng hình nón và phía dưới (vành mũ) có dạng hình vành khăn.
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Diện tích S 1 là S 1 = 2 π r h + π r 2 = 62 , 6 π r + π r 2 ( diện tích toàn phần trừ một đáy)
Diện tích S 2 là S 2 = π 11 , 1 + r 2 − π r 2 = π 123 , 21 + 22 , 2 r ( diện tích hình tròn to trừ hình tròn nhỏ)
Khi đó:
P = 3 S 2 − S 1 = 3 π 22 , 2 r + 123 , 21 − 62 , 6 π r − π r 2 = 369 , 63 π + 4 π r − π r 2
Ta có:
4 r − r 2 = 4 − 2 − r 2 ≤ 4 ⇔ π 4 r − r 2 ≤ 4 π ⇒ P ≤ 373 , 63 π
Dấu “=” xảy ra khi và chỉ khi:
r = 2 ⇒ d = 2 x + r = 2 11 , 1 + 2 = 26 , 2 ⇒ r + d = 28 , 2

Bài 6:
a: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Vì M là trung điểm của BC
nên \(MB=MC=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Ta có: ΔAMB vuông tại M
=>\(AM^2+MB^2=AB^2\)
=>\(AM^2+6^2=10^2\)
=>\(AM^2+36=100\)
=>\(AM^2=100-36=64\)
=>\(AM=\sqrt{64}=8\left(cm\right)\)
b: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Hình bình hành AMCK có \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
c: AMCK là hình chữ nhật
=>AK//CM và AK=CM
Ta có: AK//CM
M\(\in\)BC
Do đó: AK//MB
Ta có: AK=CM
CM=MB
Do đó: AK=MB
Xét tứ giác AKMB có
AK//MB
AK=MB
Do đó: AKMB là hình bình hành
d: Để hình chữ nhật AMCK trở thành hình vuông thì AM=CM
mà \(CM=\dfrac{BC}{2}\)
nên \(AM=\dfrac{BC}{2}\)
Xét ΔABC có
AM là đường trung tuyến
\(AM=\dfrac{BC}{2}\)
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
câu này đề cương trường thcs long bình dễ mà cx đi hỏi à s gà v

Diện tích vải cần có để làm nên cái mũ gồm diện tích xung quanh của hình nón và diện tích của vành nón.
Bán kính đường tròn đáy của hình nón: 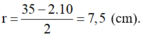
Diện tích xung quanh hình nón: Sxq = π.r.l = π.7,5.30 = 225π (cm2)
Diện tích vành nón (hình vành khăn): 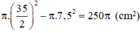
Diện tích vải cần để may: 225π + 250π = 475π ≈ 1492,3 (cm2)

Diện tích vải cần có để làm nên cái mũ gồm diện tích xung quanh của hình nón và diện tích của vành nón.
Bán kính đường tròn đáy của hình nón: 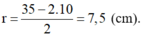
Diện tích xung quanh hình nón: Sxq = π.r.l = π.7,5.30 = 225π (cm2)
Diện tích vành nón (hình vành khăn): 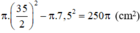
Diện tích vải cần để may: 225π + 250π = 475π ≈ 1492,3 (cm2)

Diện tích vải lều cần phủ kín các mặt bên:
S = 4 . 3 . 3,2 : 2 = 19,2 (m²)