Với giá trị nào của m thì phương trình (ẩn số x)
2mx+2=0 có nghiệm là 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x 2 - 2mx + 2m – 1 = 0
Δ = b 2 - 4ac = 2 m 2 - 4.(2m - 1) = 4 m 2 -8m + 4 = 4 m - 1 2
Do Δ = 4 m - 1 2 ≥ 0 ∀ m nên phương trình luôn có nghiệm với mọi m

a,\(\Delta'=\left(-m\right)^2-1.1=m^2-1\)
b,Để pt có nghiệm kép thì \(\Delta'=0\)
\(\Leftrightarrow m^2-1=0\Leftrightarrow m^2=1\Leftrightarrow m=\pm1\)
Vậy......


a) Δ' = m 2 - (-4m - 4) = m 2 + 4m + 4 = m + 2 2 ≥ 0 ∀m
Vậy phương trình đã cho luôn có nghiệm với mọi m

PT $(*)$ là PT bậc nhất ẩn $x$ thì làm sao mà có $x_1,x_2$ được hả bạn?
PT cuối cũng bị lỗi.
Bạn xem lại đề!

\(f'\left(x\right)=2cos2x-4\left(1-2m\right)sin2x-2m\)
Phương trình \(f'\left(x\right)=0\) có nghiệm
\(\Leftrightarrow2cos2x-4\left(1-2m\right)sin2x=2m\) có nghiệm
\(\Leftrightarrow cos2x-2\left(1-2m\right)sin2x=m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(1^2+4\left(1-2m\right)^2\ge m^2\)
\(\Leftrightarrow15m^2-16m+5\ge0\)
\(\Leftrightarrow15\left(m-\dfrac{8}{15}\right)^2+\dfrac{11}{15}\ge0\) (luôn đúng)
Vậy \(f'\left(x\right)=0\) có nghiệm với mọi m

a, với =-3
\(=>x^2-6x+6=0\)
\(\Delta=\left(-6\right)^2-4.6=12>0\)
=>pt có 2 nghiệm phân biệt x3,x4
\(=>\left[{}\begin{matrix}x3=\dfrac{6+\sqrt{12}}{2}=3+\sqrt{3}\\x4=\dfrac{6-\sqrt{12}}{2}=3-\sqrt{3}\end{matrix}\right.\)
b, \(\Delta=\left(2m\right)^2-4\left(m^2+m\right)=4m^2-4m^2-4m=-4m\)
pt đã cho đề bài có 2 nghiệm phân biệt x1,x2 khi
\(-4m>0< =>m< 0\)
theo vi ét \(=>\left\{{}\begin{matrix}x1+x2=-2m\\x1x2=m^2+m\end{matrix}\right.\)
có \(\left(x1-x2\right)\left(x1^2-x2^2\right)=32\)
\(< =>\left(x1-x2\right)^2\left(x1+x2\right)=32\)
\(< =>\left[x1^2-2x1x2+x2^2\right]\left(-2m\right)=32\)
\(< =>\left[\left(x1+x2\right)^2-4x1x2\right]\left(-2m\right)=32\)
\(< =>\left[\left(-2m\right)^2-4\left(m^2+m\right)\right]\left(-2m\right)=32< =>m=2\)(loại)
Vậy \(m\in\varnothing\)
Lời giải:
a. Với $m=-3$ thì pt trở thành:
$x^2-6x+6=0\Leftrightarrow x=3\pm \sqrt{3}$
b. Để pt có 2 nghiệm thì: $\Delta'=m^2-(m^2+m)=-m\geq 0$
$\Leftrightarrow m\leq 0$
Áp dụng định lý Viet: $x_1+x_2=-2m; x_1x_2=m^2+m$
Khi đó:
$(x_1-x_2)(x_1^2-x_2^2)=32$
$\Leftrightarrow (x_1-x_2)^2(x_1+x_2)=32$
$\Leftrightarrow [(x_1+x_2)^2-4x_1x_2](x_1+x_2)=32$
$\Leftrightarrow [(-2m)^2-4(m^2+m)](-2m)=32$
$\Leftrightarrow 8m^2=32$
$\Leftrightarrow m^2=4$
$\Rightarrow m=-2$ (do $m\leq 0$)
Vây.........

Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 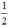
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 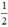
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 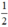
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 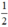 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 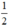 và vô nghiệm khi m >
và vô nghiệm khi m > 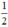
Thay x = 1 vào phương trình được:
2m+2=0
<=> 2m=-2
<=> m=-1