Biết rằng trong tất cả các cặp (x;y) thỏa mãn chỉ có duy nhất một cặp (x;y) thỏa mãn 3x+4y-m=0. Khi đó hãy tính tổng tất cả các giá trị m tìm được.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

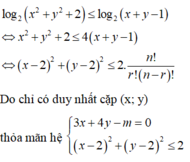
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
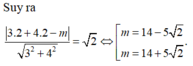
Chọn C.


a: \(\Leftrightarrow\left(x+3;y-2\right)\in\left\{\left(1;7\right);\left(7;1\right);\left(-1;-7\right);\left(-7;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(-2;9\right);\left(4;3\right);\left(-4;-5\right);\left(-10;1\right)\right\}\)
b: (x+1)(xy+2)=5
=>\(\left(x+1;xy+2\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,xy\right)\in\left\{\left(0;3\right);\left(4;-1\right);\left(-2;-7\right);\left(-6;-3\right)\right\}\)
mà x,y là số nguyên
nên (x,y)=\(\varnothing\)

Từ 1 điểm nối với n-1 điểm còn lại thì ta được tất cả n(n-1)
Mà ta thấy mỗi đoạn thẳng xuất hiện 2 lần nên có số đoạn thẳng là:\(\frac{n\left(n-1\right)}{2}=435\)
\(\Rightarrow n\left(n-1\right)=870\)
\(\Rightarrow n\left(n-1\right)=30.29\)
\(\Rightarrow n=30\)
Vậy có tất cả 30 điểm.

Ta có :n(n−1)2=1770n(n−1)2=1770.Do đó:
n(n-1)=2.1770=22.3.5.59=60.59
Vậy n =60
học tốt
Ta có :n(n−1)2=1770n(n−1)2=1770.Do đó:
n(n-1)=2.1770=22.3.5.59=60.59
Vậy n =........
chúc bn học tốt
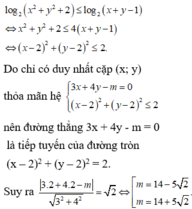
Chọn B