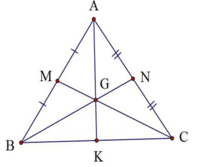
Câu 12. Tam giác ABC có MA=MB, NA=NC, BC=6 cm thì MN có số đo bằngA.12cm; B. 4cm; C. 3cm ; D. 6...
Đọc tiếp
Câu 12. Tam giác ABC có MA=MB, NA=NC, BC=6 cm thì MN có số đo bằng | |||||||||||||||||||
A.12cm | ; |
|
|
| B. 4cm | ; |
|
|
|
|
|
| C. 3cm |
| ; |
|
|
| D. 6 cm |
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
7 tháng 12 2021
Xét ΔABCΔABC có :
MA = MB ; NA = NC
=> MN là đường trung bình của ΔABCΔABC
=> MN // BC và MN = 12BC
11 tháng 1 2023
Diện tích của tam giác ABM là: 25 x 12 : 2 = 150 cm vuông
Tam giác ABM và tam giác AMN có chung chiều cao xuất phát từ đỉnh A hạ xuống BC; đáy BM = 2/3 đáy MN
=> Diện tích ABM = 2323 x Diện tích AMN
Diện tích AMN là:
Diện tích ABM : 2323 = 150 : 2323 = 225 cm vuông
+) Tam giác ANC và tam giác AMN có chung chiều cao hạ từ đỉnh A xuống cạnh BC; đáy NC = 1/2 đáy MN
=> Diện tích ANC là:
1212 x Diện tích AMN = 1212 x 225 = 112,5 cm vuông
Ta có: Diện tích tam giác ABC là: SABM + SAMN + SANC = 150 + 225 + 112, 5 = 487,5 cm2
NT
2
9 tháng 12 2016
bn ơi nếu bn cho giả thiết như thế thì mk có thể vẽ đc hình như thế này :
A B C M N
nhìn là thấy MN ko // BC được bn ạ
ai thấy mk nói đúng thì xin cho
9 tháng 12 2016
BAN SAI HINH ROI NHUNG GIA THIET CUNG CHO K RO CO THE BAN VE DUNG
CM
7 tháng 1 2017
Theo bài ra ta có diện tích ABG=ACG; Vì hai tam giác ABG và ACG có cạnh AG chung nên đường cao hạ từ B và đường cao hạ từ C sẽ bằng nhau ( *)
- Xét tam giác BGK và CGK có cạnh GK chung và từ (*) ta có đường cao hạ từ B và C bằng nhau. Do đó: Diện tích BGK và CGK bằng nhau (**)
Mặt khác ta thấy: hai tam giác BGK và CGK có chung đường cao hạ từ G (***)
- Từ ( **) và (***) ta có KB=KC ( đpcm)
19 tháng 5 2022
a; Xét ΔBAC có MN//BC
nên AM/AB=AN/AC
=>AM/20=15/20
=>AM=15
b: Xét ΔABC có MN//BC
nên AN/NC=AM/MB
=>AN/NC=3/2
=>AN/3=NC/2
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AN}{3}=\dfrac{NC}{2}=\dfrac{AN+NC}{3+2}=\dfrac{5}{5}=1\)
Do đó: NC=2
c: Xét ΔBCA có MN//BC
nên MN/BC=AM/AB
=>MN/6=8/12=2/3
hay MN=4
25 tháng 2 2022
Bài 2:
a: Xét ΔABC có MN//BC
nên AM/AB=MN/BC
=>AM/(AM+8)=2/3
=>3AM=2AM+16
=>AM=16(cm)
b: Xét ΔABC có MN//BC
nên AM/MB=AN/NC
=>10/NC=2
hay NC=5(cm)
25 tháng 2 2022
Bài 2.
a.ta có: MN//BC ( gt )
\(\Rightarrow\dfrac{MN}{BC}=\dfrac{AM}{AM+8}\) ( hệ quả Ta-lét )
\(\Leftrightarrow\dfrac{12}{18}=\dfrac{AM}{AM+8}\)
\(\Leftrightarrow2\left(AM+8\right)=3AM\)
\(\Leftrightarrow2AM+16=3AM\)
\(\Leftrightarrow AM=16\)
b.ta có: \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\) ( định lí Ta-lét )
\(\Leftrightarrow\dfrac{16}{8}=\dfrac{10}{NC}\)
\(\Leftrightarrow16NC=80\)
\(\Leftrightarrow NC=5\)
D
D