Cho hai số phức z 1 = 1 - 2 i , z 2 = x - 4 + y i với ( x , y ∈ R ) . Tìm cặp (x,y) để z 2 = 2 z 1
A. (x,y)=(4;6)
B. (x,y)=(5;-4)
C. (x,y)=(6;-4)
D. (x,y)=(6;4)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

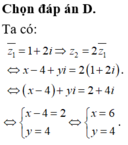

Lời giải:
\(z=x+yi\Rightarrow |z|=\sqrt{x^2+y^2}=1(1)\)
\(y=\sqrt{3}x; y>0\Rightarrow \left\{\begin{matrix} x>0\\ y^2=3x^2(2)\end{matrix}\right.\)
Từ \((1); (2)\Rightarrow \sqrt{x^2+3x^2}=1\Leftrightarrow 2x=1\Leftrightarrow x=\frac{1}{2}\)
\(\Rightarrow y=\frac{\sqrt{3}}{2}\)
Số phức \(z=\frac{1}{2}+\frac{\sqrt{3}i}{2}\)
\(\Rightarrow z-\frac{1}{z}+1=1+\sqrt{3}i\)
\(\Rightarrow |z-\frac{1}{z}+1|=\sqrt{1^2+3}=2\) (đây chính là mo đun của số phức đã cho )

ý của bài này là tìm công thức tổng quát cho dạng toán tìm số cặp x,y biết tổng của hai số là n