Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)

Đáp án C
Phương pháp
Chia cả 2 vế cho 1 + i và suy ra đường biểu diễn của số phức z
Cách giải
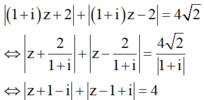
![]() Tập hợp các điểm z là elip có độ dài trục lớn là 2a=4
Tập hợp các điểm z là elip có độ dài trục lớn là 2a=4 ![]() a=2
a=2
và hai tiêu điểm ![]()


bài 1) đặc \(z=a+bi\) với \(a;b\in z;i^2=-1\)
ta có : \(\left(1+i\right)z+\overline{z}=i\Leftrightarrow\left(1+i\right)\left(a+bi\right)+\left(a-bi\right)=i\)
\(\Leftrightarrow a-b+ai+bi+a-bi=i\Leftrightarrow2a-b+ai=i\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a-b=0\\a=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
\(\Rightarrow z=1+2i\) \(\Rightarrow W=1+i+z=1+i+1+2i=2+3i\)
\(\Rightarrow\) \(modul\) của số phức \(W\) là : \(\left|W\right|=\sqrt{2^2+3^2}=\sqrt{13}\)
vậy .............................................................................................................
bài 2) đặc \(z=a+bi\) với \(a;b\in z;i^2=-1\)
ta có : \(z^2\left(1-i\right)+2\overline{z}^2\left(1+i\right)=21-i\)
\(\Leftrightarrow\left(a+bi\right)^2\left(1-i\right)+2\left(a-bi\right)^2\left(1+i\right)=21-i\)
\(\Leftrightarrow\left(a^2+2abi-b^2\right)\left(1-i\right)+2\left(a^2-2abi-b^2\right)\left(1+i\right)=21-i\)\(\Leftrightarrow a^2-a^2i+2abi+2ab-b^2+b^2i+2\left(a^2+a^2i-2abi+2ab-b^2-b^2i\right)=21-i\)
\(\Leftrightarrow a^2-a^2i+2abi+2ab-b^2+b^2i+2a^2+2a^2i-4abi+4ab-2b^2-2b^2i=21-i\)
\(\Leftrightarrow a^2-a^2i+2abi+2ab-b^2+b^2i+2a^2+2a^2i-4abi+4ab-2b^2-2b^2i=21-i\)\(\Leftrightarrow3a^2+6ab-3b^2+a^2i-2abi-b^2i=21-i\)
\(\Leftrightarrow\left(3a^2+6ab-3b^2\right)+\left(a^2-2ab-b^2\right)i=21-i\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a^2+6ab-3b^2=21\\a^2-2ab-b^2=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a^2+6ab-3b^2=21\\3a^2-6ab-3b^2=-1\end{matrix}\right.\)
\(\Rightarrow-ab=-2\Leftrightarrow-a^2b^2=-4\) và \(a^2-b^2=3\)
\(\Rightarrow a^2\) và \(-b^2\) là nghiệm của phương trình \(X^2-3X-4=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2=4\\-b^2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a^2=4\\b^2=1\end{matrix}\right.\)
\(\Rightarrow\) \(modul\) của số phức \(z\) là \(\left|z\right|=\sqrt{a^2+b^2}=\sqrt{4+1}=\sqrt{5}\)
vậy ...................................................................................................................
hôm sau phân câu 1 ; câu 2 rỏ ra nha bạn . cho dể đọc thôi ![]()

Đáp án C