Cho hàm số y = 1 4 x 4 - ( m + 1 2 ) x 2 có đồ thị (C). Có bao nhiêu giá trị thực của tham số m để (C) có ba điểm cực trị và đường tròn qua ba điểm cực trị này đồng thời đi qua điểm A( - 3 2 ;).
A. 3.
B. 1.
C. 4.
D. 2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để hàm số có ba điểm cực trị khi và chỉ khi ab< 0 hay 1.( -2m) <0
Suy ra m> 0
Khi đó
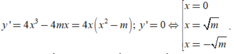
Suy ra tọa độ các điểm cực trị của đồ thị hàm số là:
A 0 ; 2 , B m ; - m 2 + 2 , C - m ; - m 2 + 2
Ycbt O A . O B . O C = 12 ⇔ 2 m + - m 2 + 2 2 = 12
Giải ra ta được m=2; có một giá trị nguyên.
Chọn B.

Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
![]()
Hai điểm cực trị có hoành độ dương
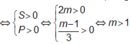
Vậy các giá trị cần tìm của m là m >1

Ta có : y’ = 4x3-4( m+ 1) x= 4x( x2- (m+ 1) ).
Hàm số có điểm cực trị khi và chỉ khi y’ = 0 có nghiệm phân biệt hay m+1> 0 suy ra m> - 1. (*)
Khi đó, ta có:
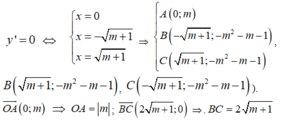
Do đó O A = B C ⇔ m = 2 m + 1 ⇔ m 2 - 4 m - 4 = 0 ( ∆ ' = 8 ) ⇔ m = 2 ± 2 2 (thỏa mãn (*)).
Vậy m = 2 ± 2 2 .
Chọn A.

Chọn A
Ta có:
![]()
Hàm số có 3 điểm cực trị khi và chỉ khi :
y ' có 3 nghiệm phân biệt
⇔ m + 1 > 0 ⇔ m > - 1 ( * )
Khi đó, ta có y ' = 0
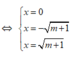
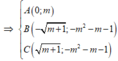
(vai trò của B, C trong bài toán là như nhau ) nên ta giả sử
![]()
Ta có: O A ( 0 ; m ) ⇒ O A = m ⇒ B C = 2 m + 1
Do đó OA = BC
![]()
![]()
⇔ m = 2 ± 2 2 ( t h ỏ a m ã n ) ( * )
Vậy m = 2 ± 2 2