Tìm tất cả các giá trị của m để hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương.
A. m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
B. m ∈ 2 - 2 7 3 ; 2 + 2 7 3
C. m ∈ - 1 ; 2
D. m ∈ - ∞ ; - 1 ∪ 2 ; + ∞

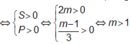
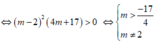
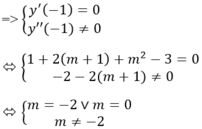
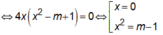
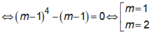
Để đồ thị hàm số có 2 điểm cực trị thì
Khi đó, do a = 1 3 > 0 nên hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương . Đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất là x = 0 1 và hai cực trị x 1 ; x 2 x 1 < x 1 thỏa mãn: 0 < x 1 < x 2 2
Ta có:
hoặc là vô nghiệm hoặc là có nghiệm kép x = 0
Kết hợp điều kiện ta có:
m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
Chọn: A