Với các số thực dương a, b bất kì, mệnh đề nào dưới đây đúng?
A. ln(ab) = lna + lnb
B. ln a b = ln a ln b
C. ln a b = ln b - ln a
D. ln(ab) = lna.lnb
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:


Đáp án B
Đặt 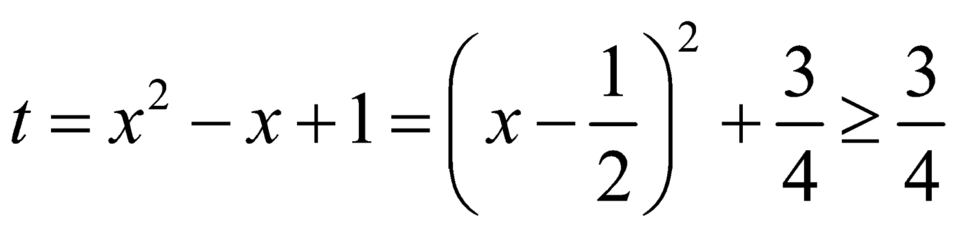
Ta có:
![]()
![]()
Đặt ![]() .
.
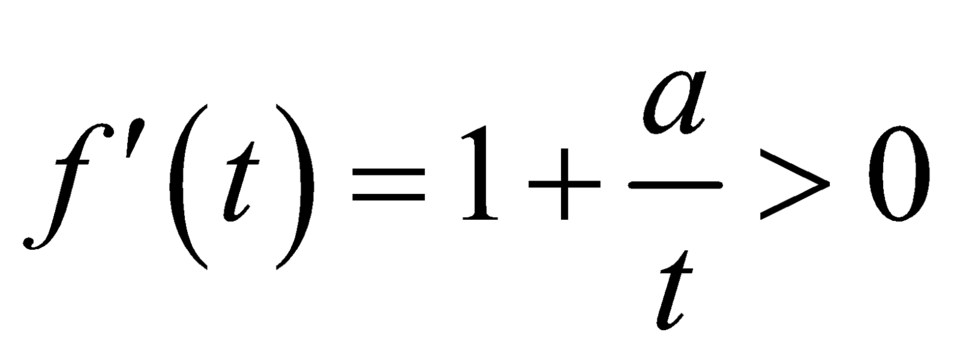
![]() là hàm số đồng biến trên
là hàm số đồng biến trên 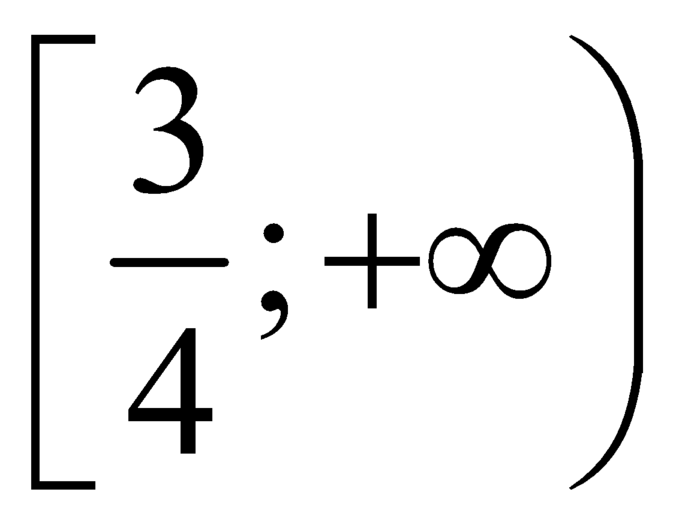 .
.
Khi đó 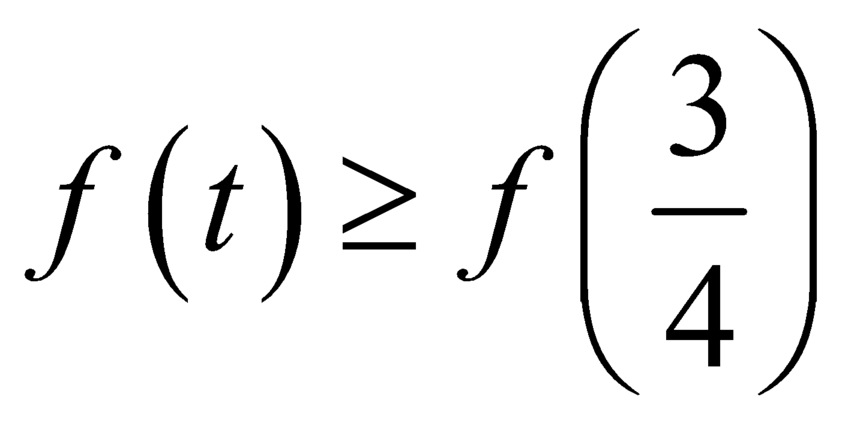
![]()
![]()
![]()

Vì \(a\ge1;b\ge1\) nên \(\ln a;\ln b\) và \(\ln\frac{a+b}{2}\) không âm. Ta có :
* \(\frac{a+b}{2}\ge\sqrt{ab}\Rightarrow\ln\frac{a+b}{2}\ge\ln\sqrt{ab}\Leftrightarrow\ln\frac{a+b}{2}\ge\frac{1}{2}\left(\ln a+\ln b\right)\) (1)
* \(\ln a+\ln b\ge2\sqrt{\ln a.\ln b}\) Áp dụng BĐT Cauchy
\(\Rightarrow2\left(\ln a+\ln b\right)\ge\ln a+\ln b+2\sqrt{\ln a.\ln b}=\left(\sqrt{\ln a}+\sqrt{\ln b}\right)^2\)
hay :
\(\ln a+\ln b\ge\frac{1}{2}\left(\sqrt{\ln a}+\sqrt{\ln b}\right)^2\) (2)
Từ (1) và (2) \(\Rightarrow\ln\frac{a+b}{2}\ge\frac{1}{4}\left(\sqrt{\ln a}+\sqrt{\ln b}\right)^2\)
hay \(\frac{\sqrt{\ln a}+\sqrt{\ln b}}{2}\le\sqrt{\ln\frac{a+b}{2}}\)
Đáp án A
Phương pháp: Sử dụng các công thức: (Giả sử các biểu thức là có nghĩa).
(Giả sử các biểu thức là có nghĩa).
Cách giải: Với các số thực dương a, b bất kì , mệnh đề đúng là: ln(ab) = lna + lnb