Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Vì OA, OB, OC đôi một vuông góc với nhau 1 d 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Với d là khoảng cách từ O -> (ABC) suy ra 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức, ta có x 2 a + y 2 b + z 2 c ≥ x + y + z 2 a + b + c
Vậy d m a x = 1 3

Đáp án B
Ta có ln x y = ln x + ln y ≥ ln x 2 + y
⇔ x y ≥ x 2 + y ⇔ y x - 1 ≥ x 2
Vì x = 1 không thỏa và y > 0 => x > 1
⇒ P = x y ≥ x 2 x - 1 + x = f x
X é t h à m s ố f x = x 2 x - 1 + x v ớ i x > 1
⇒ f ' x = x 2 - 2 x x - 1 2 + x = 2 x 2 - 4 x + 1 x - 1 2
⇒ f ' x = 0 ⇔ x = 2 + 2 2 v ì x > 1
Dựa vào bảng biến thiên của hàm số f(x) suy ra
⇒ M i n P = M i n x > 1 f x = f 1 = 3 + 2 2 .

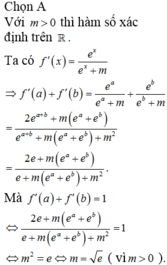

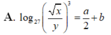
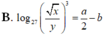
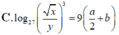
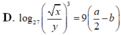
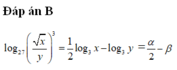
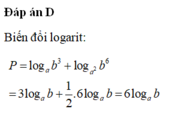
Chọn C