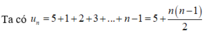Cho hàm với hàng số a > 0. Xét dãy số (un) có số hạng tổng quát Hãy tính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

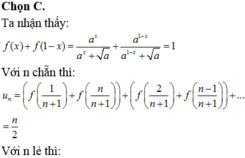
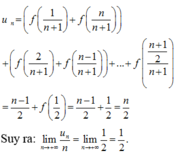

a) Năm số hạng đầu của dãy số là: \(u_1=1^2=1;u_2=2^2=4;u_3=3^2=9;u_4=4^2=16;u_5=5^2=25\).
Số hạng tổng quát của dãy số un là \(u_n=n^2\) với n ∈ ℕ.
b) Dạng khai triển của dãy số \(u_1=1,u_2=4,u_3=9,u_4=16,...u_n=n^2\) ...

Ta sẽ chứng minh dãy này giảm theo quy nạp.
Với n = 1 ta có u1 = -1
Với n = 2 ta có u2 = -5
=> u1 > u2
Giả sử dãy trên đúng với uk > uk+1 tức 2k - 3k > 2(k + 1) - 3k + 1 <=> 2k - 2(k + 1) > 3k - 3k+1
Ta cần chứng minh dãy cũng đúng với uk+1 > uk+2
Hay 2(k + 1) - 3k+1 > 2(k + 2) - 3k+2
<=> 2k - 3.3k > 2(k + 1) - 3.3k+1
<=> 2k - 2(k + 1) > 3.(3k - 3k+1)
Thật vậy: Với k nguyên dương ta luôn có 3k - 3k+1 < 0 và 3 > 1 nên 3(3k - 3k+1) < 3k - 3k+1
Lại có 2k - 2(k + 1) > 3k - 3k+1 => 2k - 2(k + 1) > 3.(3k - 3k+1) (đpcm)
Vậy dãy un trên là dãy giảm

1:
a: \(u_2=2\cdot1+3=5;u_3=2\cdot5+3=13;u_4=2\cdot13+3=29;\)
\(u_5=2\cdot29+3=61\)
b: \(u_2=u_1+2^2\)
\(u_3=u_2+2^3\)
\(u_4=u_3+2^4\)
\(u_5=u_4+2^5\)
Do đó: \(u_n=u_{n-1}+2^n\)

a. Năm số hạng đầu của dãy số
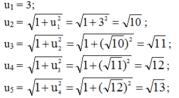
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
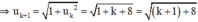
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.