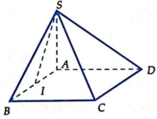
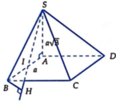
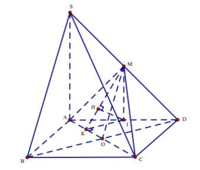
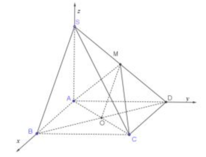
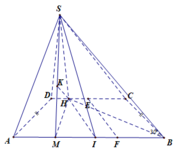
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh 2a, SA = a 3 và vuông góc với đáy, I là trung điểm của AB. Tính khoảng cách giữa SI và BC.
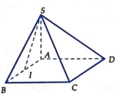
A. d ( S I ; B C ) = a .
B. d ( S I ; B C ) = a 3 4 .
C. d ( S I ; B C ) = a 3 .
D. d ( S I ; B C ) = a 3 2 .

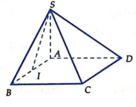
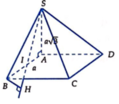
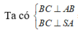


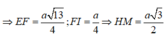
Đáp án D.
Ta có
B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ ( S A B ) ⇒ B C ⊥ S I
Gọi H là hình chiếu của B lên SI ⇒ B H ⊥ S I B H ⊥ B C ⇒ B H = d ( B C ; S I )
⇒ Δ B H I ∽ Δ S A I ⇒ B H S A = B I S I ⇒ B H = S A . B I S I = a 3 . a 2 a = a 3 2