Question

[Pham Trong Bach]

Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, A D = B C = a 13 4 ,   A B = 2 a ,   C D = 3 a 2 , mặt phẳng   (SCD) vuông góc với mặt phẳng   (ABCD). Tam giác ASI cân tại S, với I là trung điểm của cạnh AB, SB tạo với mặt phẳng   (ABCD) một góc 30º. Khoảng cách giữa SI và CD là

A. a 13 7

B. 2 a 21 7

C. 2 a 13 7

D.  a 21 7

Answer 1

[Cao Minh Tâm]

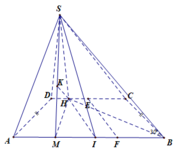
Đáp án D

Gọi M, E là trung điểm của AI và CD

Kẻ S H ⊥ C D  do mặt phẳng (SCD) vuông góc với mặt phẳng

(ABCD) nên S H ⊥ ( A B C D ) . Mặt khác SA=SI 

⇒ S M ⊥ A I ⇒ A I ⊥ ( S H M ) ⇒ H K ⊥ ( S A I )  mà CD

Song song với (SAB) ⇒ H K  là khoảng cách cần tìm.

Qua E kẻ đường thẳng song song với BC cắt AB tại F

 

⇒ H B = a 3 ;   S H = H B . tan 30 o = a 3 . 1 3 = a

Ta có 1 H K 2 = 1 S H 2 + 1 H M 2 = 1 a 2 + 4 3 a 2 = 7 3 a 2

⇒ H K = a 21 7