Giải bất phương trình log4(x2 – x – 8) < 1 + log3x được tập nghiệm là một khoảng trên trục số có độ dài là: ...
Đọc tiếp
Giải bất phương trình log4(x2 – x – 8) < 1 + log3x được tập nghiệm là một khoảng trên trục số có độ dài là:
K
Khách
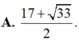
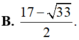
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 5 2019
Đáp án D.
Điều kiện x > 0. Phương trình đã cho tương đương với:
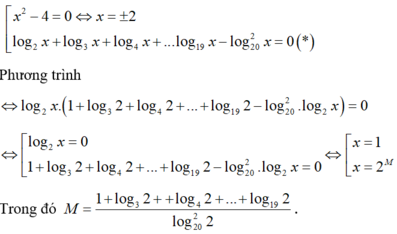
Vậy phương trình có 4 nghiệm.
KV
29 tháng 4 2022
Ta có:
\(-2018m>-2018n\)
\(\Rightarrow-2018m.\left(-\dfrac{1}{2018}\right)< -2018n.\left(-\dfrac{1}{2018}\right)\)
\(\Rightarrow m>n\)
b) \(x^2-x\left(x+2\right)>3x-1\)
\(\Leftrightarrow x^2-x^2-2x>3x-1\)
\(\Leftrightarrow-2x-3x>-1\)
\(\Leftrightarrow-5x>-1\)
\(\Leftrightarrow x< \dfrac{1}{5}\)
Vậy S = {\(x\) | \(x< \dfrac{1}{5}\)}
29 tháng 4 2022
a) Ta có: -2018m > -2018n
\(\Leftrightarrow-2018m\times\left(\dfrac{-1}{2018}\right)< -2018n\times\left(\dfrac{-1}{2018}\right)\)
\(\Leftrightarrow\) m < n
CM
29 tháng 8 2019
a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình
+) 
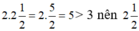không là nghiệm của bất phương trình ,
+) 2π > 3 nên π không là nghiệm của bất phương trình.
+) 
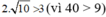nên √10 không là nghiệm của bất phương trình,
Các số là nghiệm của bất phương trình trên là: -2;
Các số không là nghiệm của bất phương trình trên là: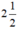 
; π; √10
b)2x ≤ 3 ⇔ x ≤ 3/2
Biểu diễn tập nghiệm trên trục số là:
CM
17 tháng 3 2018
Đáp án C
Ta có
log 3 x ≤ log 1 3 2 x ⇔ x > 0 log 3 x ≤ − log 3 2 x ⇔ x > 0 log 3 x + log 3 2 x ≤ 0
⇔ x > 0 log 3 2 x 2 ≤ 0 ⇔ x > 0 2 x 2 ≤ 1 ⇔ x > 0 − 1 2 ≤ x ≤ 1 2 ⇔ 0 < x ≤ 1 2
Vậy tập nghiệm của bất phương trình là
0 ; 1 2 → a = 0, b = 1 2 → a 2 + b 2 = 1 2
PT
1
CM
2 tháng 11 2019
Ta biểu diễn x ≥ 8 trên trục số như sau:
Đáp án cần chọn là: C
Đáp án B.
Điều kiện x > 1 + 33 2
Đặt t = log3x <=> x = 3t
Ta có bất phương trình: 9t < 4.4t + 3t + 8
⇔ 4 . 4 9 t + 1 3 t + 8 1 9 t > 1
Hàm số f ( t ) = 4 . 4 9 t + 1 3 t + 8 1 9 t nghịch biến và f(2) = 1 nên ta có t < 2 tìm được tập nghiệm là 1 + 33 2 ; 9 có độ dài trên trục số là 9 - 1 + 33 2 = 17 - 33 2 .