Cho a là số thực dương, gọi S là diện tích hình phẳng giới hạn bởi hai parabol P 1 : y = x 2 1 + a 4 và P 2 : y = 4 a 2 - 2 a x - x 2 1 + a 4 . Tìm giá trị lớn nhất của S.
A. maxS=9
B. m a x S = 27 4
C. m a x S = 9 27 4 4
D. m a x S = 9 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo giả thiết và công thức tích phân từng phần, ta có:
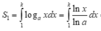
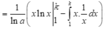
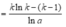
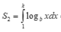
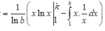
![]()
Vậy ![]()
![]()
Chọn đáp án A.

Chọn đáp án B
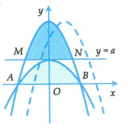
Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái một đơn vị. Khi đó, phương trình các parabol mới là
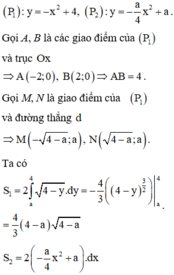
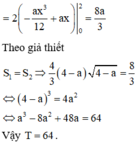

Chọn đáp án A
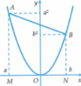
Giả sử A a ; a 2 và B b ; b 2 là hai điểm thuộc (P) và thỏa mãn AB = 2018.
Phương trình đường thẳng d đi qua hai điểm A và B là
![]()
![]()
Diện tích hình phẳng giới hạn bởi (P) và đường thẳng d là:
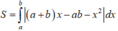
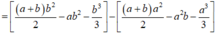
= 1 6 b - a 3
Gọi M là hình chiếu của A trên Ox và N là hình chiếu của B trên Ox. Suy ra M(a;0) và N(b;0).
Ta luôn có M N ≤ A B hay b - a = b - a ≤ 2018 .
Dấu “=” xảy ra khi MN//AB hay AB//Ox. Khi đó a = -1009; b = 1009.
Vậy S = 1 6 b - a 3 = 2018 3 6

Đáp án B
Xét phương trình
2 x 2 + 3 x + 1 = x 2 − x − 2 ⇔ x 2 + 4 x + 3 = 0 ⇔ x = − 1 x = − 3
Vậy diện tích hình phẳng cần tính là
S = ∫ − 3 − 1 x 2 + 4 x + 3 d x = ∫ − 3 − 1 x 2 + 4 x + 3 d x = 4 3
Vậy cos π S = − 2 2 .
Chọn đáp án C