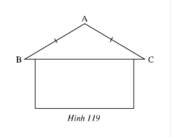
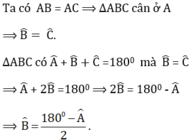Đề làm một kèo nhà bằng sắt để lợp mái tôn sao cho có độ dốc vừa phải. Người thợ thiết kế kèo hình tam giác ABC cân ( AB=AC ) có thanh AH được hàn vuông góc với thanh BC. Thanh HK được hàn vuông góc với thanh AC. Biết góc A C H ^ = 30 ° và AH=2 cm. Tính độ dài các thanh: AK, KC, HK và HC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
7 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
4 tháng 8 2023
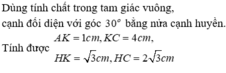
ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=48/2=24dm
AB=AC=căn AH^2+HC^2=26(dm)
Xét ΔAHB có BM/BA=BE/BH=1/2
nên ME//AH và ME=1/2AH=5dm
Xét ΔCAH có CN/CA=CF/CH
nên NF//AH
=>NF/AH=CF/CH=1/2
=>NF=5dm
ΔAHB vuông tại H có HM là trung tuyến
nên HM=AB/2=13dm
NG
20 tháng 1 2021
\(a,\text{Ta có:}AB=AC\left(gt\right)\Rightarrow\Delta ABC\text{ cân tại A}\Rightarrow\widehat{ABC}=\widehat{ACB}\left(\text{tính chất tam giác cân}\right)\)
\(\text{Xét }\Delta ABC\text{ có: }\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^o\left(\text{tổng 3 góc trong }\Delta\right)\)
\(\text{Mà }\widehat{ACB}=\widehat{ABC}\left(cmt\right),\widehat{BAC}=145^o\left(gt\right)\)
\(\Leftrightarrow145^o+2\widehat{ABC}=180^o\)
\(\)\(\Leftrightarrow2\widehat{ABC}=35^o\)
\(\Leftrightarrow\widehat{ABC}=17,5^o\)
\(\text{Vậy }\widehat{ABC}=17,5^o\)
\(b,\text{Ta có:}AB=AC\left(gt\right)\Rightarrow\Delta ABC\text{ cân tại A}\Rightarrow\widehat{ABC}=\widehat{ACB}\left(\text{tính chất tam giác cân}\right)\)
\(\text{Xét }\Delta ABC\text{ có: }\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^o\left(\text{tổng 3 góc trong }\Delta\right)\)
\(\text{Mà }\widehat{ACB}=\widehat{ABC}\left(cmt\right),\widehat{BAC}=100^o\left(gt\right)\)
\(\Leftrightarrow100^o+2\widehat{ABC}=180^o\)
\(\Leftrightarrow2\widehat{ABC}=80^o\)
\(\Leftrightarrow2\widehat{ABC}=80^o\)
\(\Leftrightarrow\widehat{ABC}=40^o\)
\(\text{Vậy }\widehat{ABC}=40^o\)
5 tháng 1 2017
a) Do AB = AC \Rightarrow tam giác ABC cân tại A
suy ra ˆABC=ˆACB
Tam giác ABC có: ˆABC+ˆACB+ˆBAC=180o
Mà ˆABC=ˆACB (cmt)
suy ra ˆABC+ˆACB+ˆBAC=180o
= ˆABC+ˆABC+ˆBAC=180o
suy ra ˆABC=(180o−145o):2=17,50
b) Giải thích hoàn toàn tương tự ta được ˆABC=(180o−100o):2=40o
5 tháng 1 2017
Ta có hình vẽ :
Ta có : AB = AC nên tam giác ABC cân ở A và có ∠A = 145 độ , do đó ∠B = ∠C
a) Trong tam giác ABC có ∠A + ∠B + ∠C = 180 độ
⇒ ∠B + ∠C = 180 độ – 145 độ = 35 độ
Vì ∠B = ∠C nên ta có 2∠B = 35 độ
⇒ ∠B = 17,5 độ
Vậy ∠ABC = 17,5 độ
b) Tương tự với ∠A = 100 độ
Vậy ∠ABC = 40 độ
25 tháng 11 2016
Xét ΔABC ta có:
 + B + C = 180o ( tổng 3 góc Δ )
145o+ B +C= 180o
B + C=180o-145o
B + C=35o (mà B = C)
Suy ra: B= C= 35o:2= 17,5o
Xét Δ ABC ta có:
 + B + C = 180o ( tổng 3 góc Δ)
100o+ B + C = 180o
B + C = 180o - 100o
B + C = 80o
Suy ra : B = C = 80o:2 = 40o
W
25 tháng 2 2020
Ta thấy: do tam giác ABC cân nên đường cao AH cũng là đường trung tuyến của tam giác ADE. Suy ra HD=HE.
Xét tam giác ADH vuông tại H. Áp dụng định lí Pytago ta có:
AH2+HD2=AD2
(1,2)2+HD2=42
1,44+HD2=16
HD2=16-1,44=14,56(m)
=>HD=\(\frac{2\sqrt{91}}{5}\)(m)
=>ED=\(\frac{4\sqrt{91}}{5}\)\(\approx\)7,6m