Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Theo định lí Pytago tam giác ADE vuông tại A
\(DE=\sqrt{AD^2+AE^2}=20cm\)
b, Ta có DE > AD > AE
=> ^A > ^E > ^D
c, Ta có \(S_{AED}=\dfrac{1}{2}.AD.AE;S_{AED}=\dfrac{1}{2}.AH.DE\)
\(\Rightarrow AH=\dfrac{AD.AE}{DE}=\dfrac{48}{5}cm\)
Theo định lí Pytago tam giác ADH vuông tại H
\(DH=\sqrt{AD^2-AH^2}=\dfrac{64}{5}cm\)
=> DH > AH

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ABC}=90^0-\widehat{ACB}=90^0-30^0\)
hay \(\widehat{ABC}=60^0\)
Ta có: ΔAHB vuông tại A(AH⊥BC)
nên \(\widehat{BAH}+\widehat{ABH}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{BAH}=90^0-\widehat{ABH}=90^0-60^0=30^0\)
Ta có: tia AH nằm giữa hai tia AB,AC
nên \(\widehat{BAH}+\widehat{CAH}=\widehat{BAC}\)
hay \(30^0+\widehat{CAH}=90^0\)
\(\Leftrightarrow\widehat{CAH}=60^0\)
Ta có: AD là tia phân giác của \(\widehat{CAH}\)(gt)
nên \(\widehat{DAC}=\dfrac{\widehat{CAH}}{2}=\dfrac{60^0}{2}=30^0\)
Vậy: \(\widehat{ABC}=60^0\); \(\widehat{DAC}=30^0\)
b) Xét ΔADH và ΔADE có
AH=AE(gt)
\(\widehat{HAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{HAE}\))
AD chung
Do đó: ΔADH=ΔADE(c-g-c)
⇒\(\widehat{AHD}=\widehat{AED}\)(hai góc tương ứng)
mà \(\widehat{AHD}=90^0\)(AH⊥HD)
nên \(\widehat{AED}=90^0\)
hay DE⊥AC(đpcm)
c) Ta có: ΔAHD=ΔAED(cmt)
nên HD=ED(hai cạnh tương ứng)
Xét ΔFHD vuông tại H và ΔCED vuông tại E có
FH=CE(gt)
HD=ED(cmt)
Do đó: ΔFHD=ΔCED(cạnh huyền-cạnh góc vuông)
⇒\(\widehat{FDH}=\widehat{CDE}\)(hai góc tương ứng)
mà \(\widehat{CDE}+\widehat{HDE}=180^0\)(hai góc kề bù)
nên \(\widehat{FDH}+\widehat{EDH}=180^0\)
⇒\(\widehat{FDE}=180^0\)
hay F,D,E thẳng hàng(đpcm)
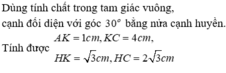

Ta thấy: do tam giác ABC cân nên đường cao AH cũng là đường trung tuyến của tam giác ADE. Suy ra HD=HE.
Xét tam giác ADH vuông tại H. Áp dụng định lí Pytago ta có:
AH2+HD2=AD2
(1,2)2+HD2=42
1,44+HD2=16
HD2=16-1,44=14,56(m)
=>HD=\(\frac{2\sqrt{91}}{5}\)(m)
=>ED=\(\frac{4\sqrt{91}}{5}\)\(\approx\)7,6m