Số giá trị nguyên của tham số m để hàm số y = m x 4 - m - 3 x 2 + m 2 không có điểm cực đại là:
A. 2
B. Vô số
C. 0
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=4x^3+12mx^2+6\left(m+1\right)x=2x\left[2x^2+6mx+3\left(m+1\right)\right]\)
Hàm có cực tiểu mà ko có cực đại khi và chỉ khi \(y'=0\) có đúng 1 nghiệm đơn
TH1: \(2x^2+6mx+3\left(m+1\right)=0\) có nghiệm \(x=0\)
\(\Leftrightarrow m=-1\)
TH2: \(2x^2+6mx+3\left(m+1\right)=0\) có ít hơn 2 nghiệm
\(\Leftrightarrow\Delta'=9m^2-6\left(m+1\right)\le0\)
\(\Leftrightarrow\dfrac{1-\sqrt{7}}{3}\le m\le\dfrac{1+\sqrt{7}}{3}\)

Chọn đáp án A
Đồ thị hàm số y=f(x-2019) được tạo thành bằng cách tịnh tiến đồ thị hàm số y=f(x) theo chiều song song với trục Ox sang bên phải 2019 đơn vị.
Đồ thị hàm số y=f(x-2019)+m-2 được tạo thành bằng cách tịnh tiến đồ thị hàm số y=f(x-2019) theo chiều song song với trục Oy lên trên m-2 đơn vị.
Đồ thị hàm số y=|f(x-2019)+m-2| được tạo thành bằng cách giữ nguyên phần đồ thị y=f(x-2019)+m-2 phía trên trục Ox, lấy đối xứng toàn bộ phần đồ thị phía dưới trục Ox qua trục Ox và xóa đi phần đồ thị phía dưới trục Ox.
Do đó để đồ thị hàm số y=|f(x-2019)+m-2| có 5 điểm cực trị thì đồ thị hàm số y=f(x-2019)+m-2 có


Hàm số y = f x với f(x) là hàm đa thức bậc 3 có 5 điểm cực trị khi và chỉ khi hàm số f(x) có hai cực trị và đồ thị của hàm số cắt trục hoành tại 3 điểm phân biệt.
Mặt khác, f(x) là hàm số bậc 3 nên khi đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt thì hàm số đồng thời cũng có hai cực trị. Do đó ta chỉ cần tìm điều kiện để phương trình f(x) = 0 có 3 nghiệm phân biệt.

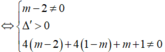
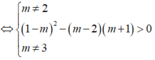
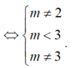

Chọn D

\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)
Hàm có 2 cực trị khi:
\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)
\(\Rightarrow-2m^2-4m+7>0\)
\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)
\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)
Chọn D.
⇒ Hàm số đạt cực tiểu tại x = 0
⇒ Khi m = 0 hàm số không có cực đại
⇒ m = 0 thỏa mãn
Ta có
Để hàm số y = m x 4 - m - 3 x 2 + m 2 không có điểm cực đại
+) (*) vô nghiệm
⇒ Hàm số chỉ có 1 cực trị x = 0
Để x = 0 là điểm cực tiểu
⇔ m < 3
⇒ 0 < m < 3
+) (*) có nghiệm kép x = 0 ⇒ m = 3
Khi đó y ' = 12 x 3 = 0 ⇔ x = 0
Qua điểm x = 0 ta thấy y ' đổi dấu từ âm sang dương
⇒ x = 0 là điểm cực tiểu
⇒ m = 3 thỏa mãn.
+) (*) có 2 nghiệm phân biệt
⇒ Hàm số luôn có cực đại ⇒ Loại.
Vậy để hàm số đã cho không có cực đại thì 0 ≤ m ≤ 3
Mà m ∈ Z ⇒ m ∈ 0 ; 1 ; 2 ; 3