Cho phương trình: x2 - x - 2 = 0.
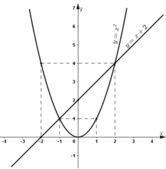
Vẽ hai đồ thị y = x2 và y = x + 2 trên cùng một hệ trục tọa độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) x 2 – x – 2 = 0
Có a = 1; b = -1; c = -2 ⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 2.
Vậy tập nghiệm của phương trình là S = {-1; 2}
b) + Đường thẳng y = x + 2 cắt trục Ox tại (-2; 0) và cắt Oy tại (0; 2).
+ Parabol y = x 2 đi qua các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4).
c) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
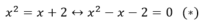
Phương trình (*) chính là phương trình đã giải ở ý (a) Do đó hai nghiệm ở câu (a) chính là hoành độ giao điểm của hai đồ thị

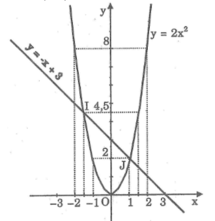
*Vẽ đồ thị hàm số y = 2 x 2
| x | -2 | -1 | 0 | 1 | 2 |
| y = 2 x 2 | 8 | 2 | 0 | 2 | 8 |
*Vẽ đồ thị hàm số y = -x + 3
Cho x = 0 thì y = 3 ⇒ (0; 3)
Cho y = 0 thì x = 3 ⇒ (3; 0)

- Bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
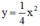 |
4 | 1 | 0 | 1 | 4 |
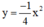 |
-4 | -1 | 0 | -1 | -4 |
- Vẽ đồ thị:
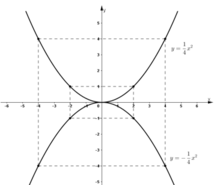
Đường thẳng qua B(0; 4) song song với Ox cắt đồ thị tại hai điểm M, M' (xem hình). Từ đồ thị ta có hoành độ của M là x = 4, của M' là x = - 4.
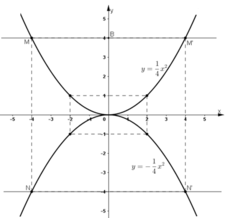

Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2y=1\\-2x+4y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=2\\-2x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y=-8\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1-2y=1-2\cdot\left(-1\right)=3\end{matrix}\right.\)

Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2y=1\\-2x+4y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=2\\-2x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8y=-8\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1-2y=1-2\cdot\left(-1\right)=3\end{matrix}\right.\)

Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2y=1\\-2x+4y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=2\\-2x+4y=-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2y=1\\8y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1-2y=3\\y=-1\end{matrix}\right.\)

b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=-x+2\)
\(\Leftrightarrow x^2+x-2=0\)(1)
a=1; b=1; c=-2
Vì a+b+c=0 nên phương trình (1) có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{-2}{1}=-2\)
Thay x=1 vào (d), ta được:
y=-1+2=1
Thay x=-2 vào (d), ta được:
y=-(-2)+2=2+2=4
Vậy: (P) và (d) có hai tọa độ giao điểm là (1;1) và (-2;4)
+ Đường thẳng y = x + 2 cắt trục Ox tại (-2; 0) và cắt Oy tại (0; 2).
+ Parabol y = x2 đi qua các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4).