Cho hàm số f(x) = (x2-m)/(x-1) (m ≠ 1)
A,y = x4 – 2x2 – 5.
B,Hàm số luôn giảm trên tập xác định.
C,Hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1.
D,Hàm số luôn tăng trên (-∞;1) và (1;+∞).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: Để (d) vuông góc với (Δ) thì \(\left(6m+1\right)\cdot6=-1\)
\(\Leftrightarrow6m+1=-\dfrac{1}{6}\)
hay \(m=-\dfrac{7}{36}\)

Đáp án C.
Ta có
y = − x 3 + x 2 − 3 x + 1 ⇒ y ' = − 3 x 2 + 2 x − 3 < 0 ; ∀ x ∈ ℝ
suy ra hàm số nghịch biến trên ℝ

Chọn B.
Hàm số (I): ![]() , ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
, ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
Hàm số (II): y’ = -4x3 + 2x. y' = 0 <=> - 4x3 + 2x = 0 <=> 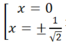 nên hàm số không đồng biến trên khoảng xác định của nó.
nên hàm số không đồng biến trên khoảng xác định của nó.
Hàm số (III): y’ = 3x2 – 3.
y’ = 0 <=> 3x2 – 3 = 0 <=> x = ±1 nên hàm số không đồng biến trên khoảng xác định của nó.


a: TXĐ: D=R
x^2;sin x đều liên tục trên R
=>f(x) liên tục trên R
b: TXĐ: D=R\{1}
x^4;-x^2;6/x-1 đều liên tục khi x thuộc (-vô cực;1) hoặc (1;+vô cực)
=>g(x) liên tục trên (-vô cực;1) và (1;+vô cực)
c: ĐKXĐ: x<>3; x<>-4
HS \(\dfrac{2x}{x-3}\) liên tục trên (-vô cực;3) và (3;+vô cực)
(x-1)/(x+4) liên tục trên (-vô cực;-4) và (-4;+vô cực)
=>h(x) liên tục trên từng khoảng xác định của nó

a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)

Đáp án C
Đáp án: Hàm số y = x 2 − 2 x − 3 không có đạo hàm tại x = 0
Hàm số y = x 2 − 1 − 4 không có đạo hàm tại x = ± 1. Hàm số y = − x 4 + 2 x 2 − 3 có lim x → ± ∞ = − ∞
Nên bảng biến thiên trên không là bảng biến thiên của 3 hàm số trên. y = x 4 − 2 x 2 − 3
Kiểm tra ta có đó là bảng biến thiên của hàm số: y = x 4 − 2 x 2 − 3

Đáp án A
Phương pháp giải:
Giải phương trình f’ bằng 0, tìm nghiệm và lập bảng biến thiên xét điểm cực trị
Lời giải:
Ta có ![]()
![]()
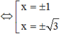
Dễ thấy f’(x) đổi dấu khi đi qua 3 điểm ![]() => Hàm số có 3 điểm cực trị.
=> Hàm số có 3 điểm cực trị.