Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Hàm số (I): ![]() , ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
, ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
Hàm số (II): y’ = -4x3 + 2x. y' = 0 <=> - 4x3 + 2x = 0 <=> 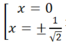 nên hàm số không đồng biến trên khoảng xác định của nó.
nên hàm số không đồng biến trên khoảng xác định của nó.
Hàm số (III): y’ = 3x2 – 3.
y’ = 0 <=> 3x2 – 3 = 0 <=> x = ±1 nên hàm số không đồng biến trên khoảng xác định của nó.

a) y = x 3 − (m + 4) x 2 − 4x + m
⇔ ( x 2 − 1)m + y − x 3 + 4 x 2 + 4x = 0
Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:
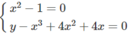
Giải hệ, ta được hai nghiệm:
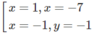
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).
b) y′ = 3 x 2 − 2(m + 4)x – 4
Δ′ = ( m + 4 ) 2 + 12
Vì Δ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
c) Học sinh tự giải.
d) Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
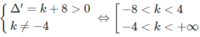

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

\(y'=-x^2-2\left(m-2\right)x+m-2\)
Hàm nghịch biến trên TXĐ khi và chỉ khi \(y'\le0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(đúng\right)\\\Delta'=\left(m-2\right)^2+m-2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left(m-2\right)\left(m-1\right)\le0\)
\(\Leftrightarrow1\le m\le2\)

Đáp án A
![]()
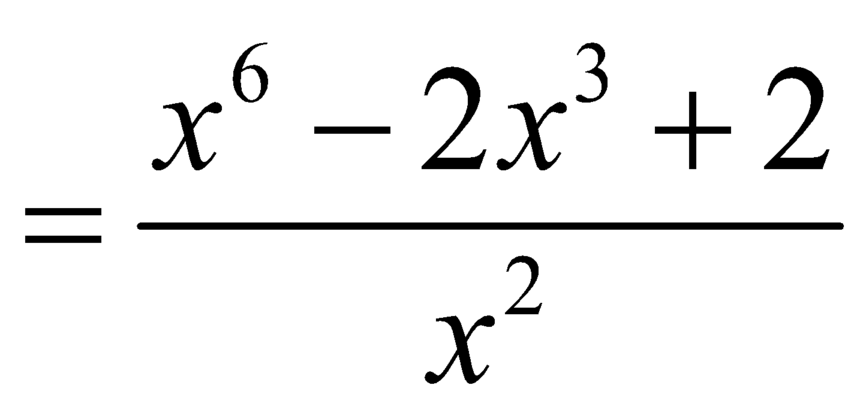
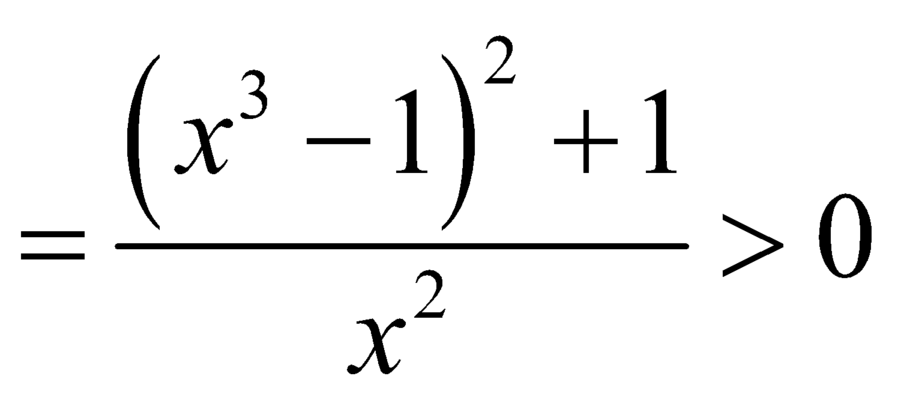 ,
, ![]() .
.
![]() đồng biến trên
đồng biến trên ![]() .
.
![]() có nhiều nhất
có nhiều nhất ![]() nghiệm trên khoảng
nghiệm trên khoảng ![]()
![]() .
.
Mặt khác ta có:
![]() ,
, ![]()
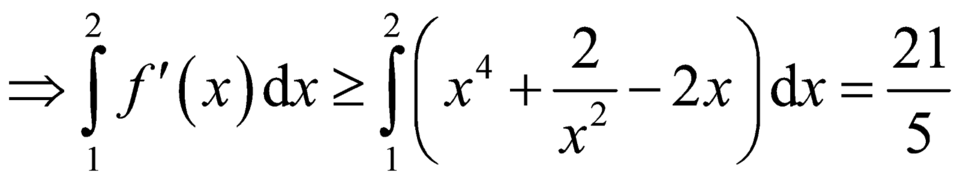
khoảng (1;2)
![]()
![]() .
.
Kết hợp giả thiết ta có ![]() liên tục trên
liên tục trên ![]() và
và ![]()
![]() .
.
Từ (1) và (2) suy ra phương trình f(x) = 0 có đúng 1 nghiệm trên khoảng (1;2)

y = 2x2 + 2mx + m -1 (Cm). Đây là hàm số bậc hai, đồ thị là parabol quay bề lõm lên phía trên.
a) m = 1 ⇒ y = 2x2 + 2x
Tập xác định D = R
\(\lim\limits_{x\rightarrow+\infty}y\left(x\right)=\lim\limits_{x\rightarrow-\infty}=+\infty\)
Bảng biến thiên:
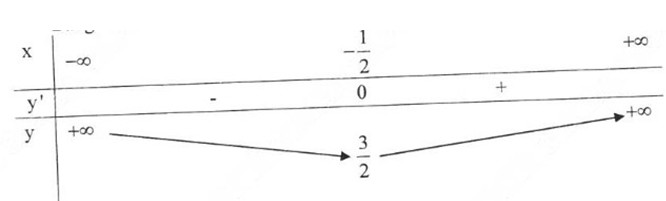
Đồ thị hàm số:
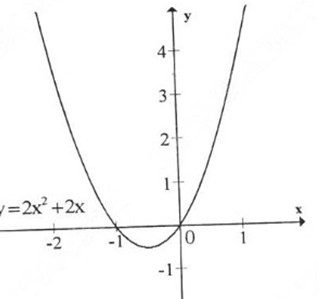
b) Tổng quát y = 2x2 + 2mx + m -1 có tập xác định D = R
y′=4x+2m=0⇔\(x=-\dfrac{m}{2}\).
Suy ra y’ > 0 với \(x>-\dfrac{m}{2}\) và \(y'< 0\) với \(x< -\dfrac{m}{2}\) tức là hàm số nghịch biến trên \(\left(-\infty;\dfrac{-m}{2}\right)\) và đồng biến trên \(\left(-\dfrac{m}{2};+\infty\right)\)
i) Để hàm số đồng biến trên khoảng (-1, +∞) thì phải có điều kiện (−1,+∞)∈(−\(\dfrac{m}{2}\),+∞)
Hay \(-\dfrac{m}{2}< -1\)\(\Leftrightarrow m>2\)
ii) Hàm số đạt cực trị tại \(x=\dfrac{m}{2}\)
Để hàm số đạt cực trị trong khoảng (-1, +∞), ta phải có:
\(-\dfrac{m}{2}\in\left(-1;+\infty\right)\) hay \(-\dfrac{m}{2}>-1\Leftrightarrow m< 2\).
c) (Cm) luôn cắt Ox tại hai điểm phân biệt
⇔ phương trình 2x2 + 2mx + m – 1 = 0 có hai nghiệm phân biệt.
Ta có:
Δ’ = m2 – 2m + 2 = (m-1)2 + 1 > 0 ∀m
Vậy (Cm) luôn cắt O x tại hai điểm phân biệt.