Tìm tất cả các giá trị của n thỏa mãn P n . A n 2 + 72 = 6 . ( A n 2 + 2 P n ) .
A. n = -3; n= 3; n= 4
B. n = 3; n= 4
C. n = 3
D. n= 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DA
20 tháng 2 2020
Bài 2:
a) Để B là phân số thì n -3 \(\ne\)0 => n\(\ne\)3
b) Để B có giá trị là số nguyên thì n+4 \(⋮\)n-3
\(\frac{n+4}{n-3}\)= \(\frac{n-3+7}{n-3}\)= \(\frac{7}{n-3}\)Vì n+4 \(⋮\)n-3 nên 7 \(⋮\)n-3
=> n-3 \(\in\)Ư(7) ={ 1;7; -1; -7}
=> n\(\in\){ 4; 10; 2; -4}
Vậy...
c) Bn thay vào r tính ra
NB
1
3 tháng 6 2018
Baif1:
Vì biểu thức trên cần lớn hơn 1,nên ta có bất phương trình :
\(\frac{x}{x-6}-\frac{6}{x-9}>1\)
\(\Leftrightarrow\frac{x^2-15x+36}{\left(x-6\right)\left(x-9\right)}\ge\frac{x^2-15x+54}{\left(x-6\right)\left(x-9\right)}\)
\(\Leftrightarrow\frac{x^2-15x+36-\left(x^2-15x+54\right)}{\left(x-6\right)\left(x-9\right)}>0\)
\(\Leftrightarrow\frac{-18}{\left(x-6\right)\left(x-9\right)}>0\)
Vì \(-18< 0\Rightarrow\left(x-6\right)\left(x-9\right)< 0\)
Xét hai trường hợp:
TH1:\(\orbr{\begin{cases}x-6>0\\x-9< 0\end{cases}\Leftrightarrow\orbr{\begin{cases}x>6\\x< 9\end{cases}}}\)
\(\Leftrightarrow6< x< 9\)(tm)(1)
TH2:\(\orbr{\begin{cases}x-6< 0\\x-9>0\end{cases}\Leftrightarrow\orbr{\begin{cases}x< 6\\x>9\end{cases}\Leftrightarrow}9< x< 6\left(ktm\right)}\)(2)
Từ (1) và (2) \(\Rightarrow6< x< 9\) lại có \(x\in Z\Rightarrow x\in\left\{7;8\right\}\)
Bài 2:
Ta có:\(2\left(n+2\right)^2+n\left(1-n\right)\ge\left(n-5\right)\left(n+5\right)\)
\(\Leftrightarrow2n^2+8n+8+n-n^2\ge n^2-25\)
\(\Leftrightarrow2n^2-n^2-n^2+8n+n\ge-25-8\)
\(\Leftrightarrow9n\ge-33\)
\(\Leftrightarrow n\ge\frac{-33}{9}\)(1)
Để n không âm thỏa mãn 7-3n là số nguyên,thì \(3n\in Z\Rightarrow n\inℤ+\)(2)
Từ (1) và (2) \(\Rightarrow n\in\left\{0;1;2;............\right\}\)
Đề bài 2 có sai không vậy chứ nó có nhiều sỗ quá bạn ạ
VV
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 12 2022
6 ⋮ n -2
n- 2 ϵƯ(6) = { -6; -3; -2; -1; 1; 2; 3; 6}
n - 2 = -6 => n = -6 + 2 => n = -4 (loại)
n- 2 = - 3 => n = 2 - 3 => n = -1 (loại)
n- 2 = -2 => n = 2 - 2 => n = 0 (thỏa mãn)
n - 2 = -1 => n = 2 - 1 => n = 1 (thỏa mãn)
n - 2 = 1 => n = 2 + 1 => n = 3 (thỏa mãn)
n - 2 = 2 => n = 2 + 2 => n = 4 (thỏa mãn)
n - 2 = 3 => n = 2 + 3 => n = 5 (thỏa mãn)
n - 2 = 6 => n = 3 + 6 => n = 9 (thỏa mãn)
kết luận n ϵ { 1; 3; 4; 5; 6}
HA
1
30 tháng 1 2016
10 chia hết cho n-2 => n -2 E Ư(10) cò n lại tự tí nh ha
Chọn B
Điều kiện: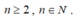
Ta có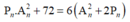
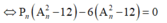
So với điều kiện, các giá trị cần tìm là n = 3; n = 4