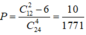Một bảng vuông gồm ô vuông đơn vị. Chọn ngẫu nhiên một ô hình chữ nhật. Tính xác suất để ô được chọn là hình vuông (trong kết quả lấy 4 chữ số ở phần thập phân).
A. 0,0134
B. 0,0133
C. 0,0136
D. 0,0132
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 5 2018
Đúng(0)
Những câu hỏi liên quan
HT
26 tháng 12 2020
Câu 1 cách làm theo như khả năng tính toán chệch 100% của mình thì....dài kinh khủng khiếp luôn á bro :D Nên mình chỉ làm câu 2 thôi nhó
Điền 9 số vào 9 ô vuông \(\Rightarrow n\left(\Omega\right)=9!\)
Gọi A là biến cố “Mỗi hàng, mỗi cột đều có ít nhất 1 số lẻ”
\(\Rightarrow\overline{A}\): “Tồn tại hàng hoặc cột không có số lẻ” <này là biến cố xung khắc của biến cố A đó nhó>
Do chỉ có 4 số chẵn nên chỉ có thể xảy ra trường hợp có 1 hàng hoặc 1 cột không có số lẻ.
*Hàng thứ nhất không có số lẻ
Chọn 3 số chẵn trong 4 số chẵn điền vào hàng đầu tiên có:
\(A^3_4\)(cách)
6 số còn lại điền vào 6 ô còn lại có 6! Cách
\(\Rightarrow A^3_4.6!\) (cách)
*Tương tự 2 hàng còn lại và 3 cột còn lại
\(n\left(\overline{A}\right)=6.24.6!\)
\(\Rightarrow P\left(\overline{A}\right)=\dfrac{6.24.6!}{9!}=...\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=...\)
CM
14 tháng 10 2017
Đáp án A
Chọn ngẫu nhiên 4 đỉnh trong 20 đỉnh có C 20 4 cách ⇒ n Ω = 4845
Đa giác 20 cạnh có 10 đường chéo đi qua tâm mà cứ 2 đường chéo đi qua tâm tạo thành một hình chữ nhật. Suy ra số hình chữ nhật tạo từ 10 đường chéo là C 10 2 = 45
Tuy nhiên trong 45 hình chữ nhật này có 5 hình vuông Số hình chữ nhật cần tính là 40
Vậy xác suất cần tính là P = 40 n Ω = 40 4845 = 8 969
CM
12 tháng 6 2019
Đáp án A
Chọn ngẫu nhiên 4 đỉnh trong 20 đỉnh có C 20 4 cách => n ( Ω ) = 4845
Đa giác 20 cạnh có 10 đường chéo đi qua tâm mà cứ 2 đường chéo đi qua tâm tạo thành một hình chữ nhật. Suy ra số hình chữ nhật tạo từ 10 đường chéo là C 10 2 = 45 .
Tuy nhiên trong 45 hình chữ nhật này có 5 hình vuông => Số hình chữ nhật cần tính là 40
Vậy xác suất cần tính là P = 40 n ( Ω ) = 40 4845 = 8 969 .
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
6 tháng 8 2023
Em viết chữ nắn nót nha chứ k đọc được ấy
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
- Cách đặt ngẫu nhiên 4 viên bi vào 9 ô là: \(C_9^4 = 126\)(cách)
- Số cách đặt 4 viên sao cho hàng nào và cột nào cũng có bi là
+ Trường hợp 1: 2 viên bi sát nhau, 2 viên bi còn lại không sát nhau: \(\left( {\left( {C_4^1 \times 2} \right) + 1 \times 4} \right) \times \left( {2 \times 1 + 1 \times 3} \right) = 60\)
+ Trường hợp 2: 3 viên bi tạo thành 1 đường chéo và không có viên nào sát nhau: 4 (Cách)
+ Trường hợp 3: 4 viên bi tạo thành 1 đường tròn lấy ô chính giữa làm tâm: 1 (cách)
=> Có 65 cách
- Xác suất để đặt 4 viên bi sao cho hàng nào cột nào cũng có bi là: \(P = \frac{{65}}{{126}}\)
CM
17 tháng 3 2017
Chọn đáp án D
Phương pháp
Nhận xét rằng: Đa giác đều có số đỉnh chẵn luôn tồn tại đường kính của đường tròn ngoại tiếp đa giác là đoạn nối hai đỉnh của đa giác.
Nên ta chia đường tròn ngoại tiếp đa giác đều đó thành hai nửa đường tròn và dựa vào tính đối xứng của các đỉnh để tạo thành một hình chữ nhật.
Tính số hình vuông trong các hình chữ nhật đó để tính xác suất 4 đỉnh tạo thành hình chữ nhật mà không phải hình vuông.
Cách giải
Số phần tử của không gian mẫu n Ω = C 24 4
Ta vẽ đường tròn ngoại tiếp đa giác đều 24 đỉnh. Vẽ một đường kính của đường tròn này. Khi đó hai nửa đường tròn đều chứa 12 đỉnh.
Với mỗi đỉnh thuộc nửa đường tròn thứ nhất ta đều có một đỉnh đối xứng với nó qua đường kính và thuộc nửa đường tròn còn lại.
Như vậy cứ hai đỉnh thuộc nửa đường tròn thứ nhất ta xác định được hai đỉnh đối xứng với nó qua đường kính và thuộc nửa đường tròn còn lại, bốn đỉnh này tạo thành một hình chữ nhật.
Vậy số hình chữ nhật có 4 đỉnh là các đỉnh của đa giác đã cho là C 12 2 .
Nhận thấy rằng trong số các hình chữ nhật tạo thành có 24:4=6 hình vuông (vì hình chữ nhật có các cạnh bằng nhau là hình vuông)
Nên số hình chữ nhật mà không phải hình vuông là C 12 2 - 6 .
Xác suất cần tìm là
