Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 cách làm theo như khả năng tính toán chệch 100% của mình thì....dài kinh khủng khiếp luôn á bro :D Nên mình chỉ làm câu 2 thôi nhó
Điền 9 số vào 9 ô vuông \(\Rightarrow n\left(\Omega\right)=9!\)
Gọi A là biến cố “Mỗi hàng, mỗi cột đều có ít nhất 1 số lẻ”
\(\Rightarrow\overline{A}\): “Tồn tại hàng hoặc cột không có số lẻ” <này là biến cố xung khắc của biến cố A đó nhó>
Do chỉ có 4 số chẵn nên chỉ có thể xảy ra trường hợp có 1 hàng hoặc 1 cột không có số lẻ.
*Hàng thứ nhất không có số lẻ
Chọn 3 số chẵn trong 4 số chẵn điền vào hàng đầu tiên có:
\(A^3_4\)(cách)
6 số còn lại điền vào 6 ô còn lại có 6! Cách
\(\Rightarrow A^3_4.6!\) (cách)
*Tương tự 2 hàng còn lại và 3 cột còn lại
\(n\left(\overline{A}\right)=6.24.6!\)
\(\Rightarrow P\left(\overline{A}\right)=\dfrac{6.24.6!}{9!}=...\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=...\)

Chọn B
Ta có ![]()
Xét A ¯ : Có ít nhất một hàng hoặc một cột chỉ toàn số chẵn.
Vì chỉ có 4 số chẵn là 2, 4, 6, 8 nên chỉ có thể có đúng một hàng hoặc đúng một cột chỉ toàn các số chẵn. Để điền như vậy cần chọn một trong số ba hàng hoặc ba cột rồi chọn 3 số chẵn xếp vào hàng hoặc cột đó, 6 số còn lại xếp tùy ý. Do đó ![]()
Vậy ![]()

Số phần tử của không gian mẫu là: ![]()
Ta tính số phần tử của không gian thuận lợi
· Cả hai bạn đều lấy ra 3 viên bi trắng có ![]()
· Cả hai bạn lấy ra 1 bi trắng và 2 bi đỏlà: ![]()
· Cả hai bạn lấy ra 2 bi trắng và 1 bi đỏ: ![]()
Số kết quả thuận lợi là n(A)=3136+64+3136=6336
Xác suất biến cố là : P(A) = 11/25
Chọn A.

Chọn C
Số phần tử của không gian mẫu ![]()
Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”.
A ¯ là biến cố “có một hàng, hoặc một cột đều là số chẵn”
Vì có 4 số chẵn nên chỉ có một hàng hoặc một cột xếp toàn số chẵn
Có 6 cách chọn ra một hàng hoặc hoặc một cột để xếp 3 số chẵn.
Có 6 cách chọn một ô không thuộc hàng đó để xếp tiếp 1 số chẵn nữa
Có 4! cách xếp 4 số chẵn và 5! xếp 5 số lẻ.
Vậy xác xuất ![]() .
.

Đáp án B
Số phần tử của không gian mẫu là: ![]()
Gọi X là biến cố “cả hai bạn Việt và Nam nằm chung một bảng đấu’
Số kết quả thuận lợi cho biến cố X là: ![]()
Vậy xác suất cần tính
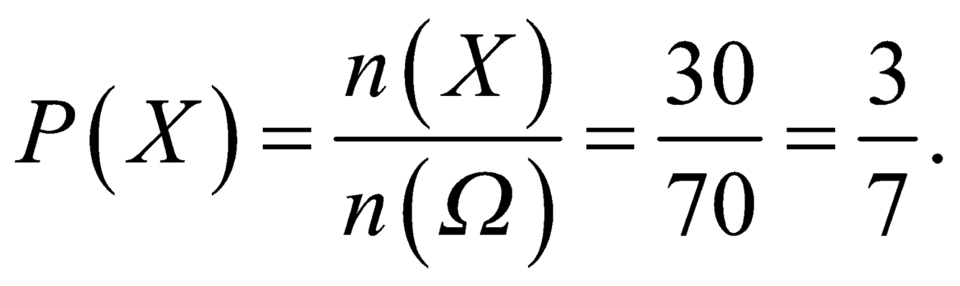




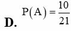



.png)
Em viết chữ nắn nót nha chứ k đọc được ấy
- Cách đặt ngẫu nhiên 4 viên bi vào 9 ô là: \(C_9^4 = 126\)(cách)
- Số cách đặt 4 viên sao cho hàng nào và cột nào cũng có bi là
+ Trường hợp 1: 2 viên bi sát nhau, 2 viên bi còn lại không sát nhau: \(\left( {\left( {C_4^1 \times 2} \right) + 1 \times 4} \right) \times \left( {2 \times 1 + 1 \times 3} \right) = 60\)
+ Trường hợp 2: 3 viên bi tạo thành 1 đường chéo và không có viên nào sát nhau: 4 (Cách)
+ Trường hợp 3: 4 viên bi tạo thành 1 đường tròn lấy ô chính giữa làm tâm: 1 (cách)
=> Có 65 cách
- Xác suất để đặt 4 viên bi sao cho hàng nào cột nào cũng có bi là: \(P = \frac{{65}}{{126}}\)