Hệ số x 6 trong khai triển đa thức P(x) = ( 5 - 3 x ) 10 có giá trị bằng đại lượng nào sau đây?
A . C 10 4 . 5 6 . 3 4
B . - C 10 6 . 5 6 . 3 4
C . - C 10 4 . 5 6 . 3 4
D . C 10 6 . 5 6 . 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo de ta co:
y1/x1 = y2/x2
=> y1/x1 = y2/x2 = (y1+y2) / (x1+x2) = (-10/3)/(5/3) = -2
=> y1=-2.x1 ; y2=-2.x2
Váy: x liên hệ với y theo công thức y=-2.x hay x = -1/2.ý

Hệ số của x5 trong khai triển x(1-2x)5 là (-2)4.C54
Hệ số của x5 trong khai triển x2(1+3x)10 là 33.C103
Do đó hệ số của x5 trong khai triển x(1-2x)5+ x2(1+3x)10 là
(-2)4.C54 + 33.C103= 3320
Chọn C

\(1.\)
\(-17-\left(x-3\right)^2\)
Ta có: \(\left(x-3\right)^2\ge0\)với \(\forall x\)
\(\Leftrightarrow-\left(x-3\right)^2\le0\)với \(\forall x\)
\(\Leftrightarrow17-\left(x-3\right)^2\le17\)với \(\forall x\)
Dấu '' = '' xảy ra khi:
\(\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(Max=-17\)khi \(x=3\)
\(2.\)
\(A=x\left(x+1\right)+\frac{3}{2}\)
\(A=x^2+x+\frac{3}{2}\)
\(A=\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
\(\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
Vậy \(Max=\frac{5}{4}\)khi \(x=\frac{-1}{2}\)

cho x và y là hai đại lượng tỉ lệ thuận, biết rằng hai giá trị bất kì x1,x2 của x có tổng bằng 1, hai giá trị tương ứng y1,y2 của y có tổng bằng 5
a, hãy biểu diễn y theo x
b, tính giá trị của x khi y=-4 , y= -1 và 1 phần 2
c, giá trị của y khi x=-4, x=0,5
ht
cho x và y là hai đại lượng tỉ lệ thuận, biết rằng hai giá trị bất kì x1,x2 của x có tổng bằng 1, hai giá trị tương ứng y1,y2 của y có tổng bằng 5
a, hãy biểu diễn y theo x
b, tính giá trị của x khi y=-4 , y= -1 và 1 phần 2

\(=\left(3x^2+1\right)^{10}\left(x+1\right)^{10}\)
Do tất cả các số hạng chứa x trong khai triển \(\left(3x^2+1\right)^{10}\) đều mũ chẵn và số hạng tự do duy nhất bằng 1
\(\Rightarrow\) Hệ số của số hạng chứa \(x^5\) bằng hệ số của số hạng chứa \(x^5\) trong khai triển \(\left(x+1\right)^{10}\)
Theo khai triển nhị thức Newton thì hệ số này bằng 252
Chọn D
Số hạng tổng quát trong khai triển là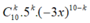
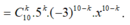 .
.
Số hạng này chứa x 6 khi 10 - k = 6 => k = 4.
Do đó hệ số x 6 trong khai triển là: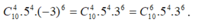 .
.