Giá trị của biểu thức A = tan 11 ° . tan 15 ° . tan 19 ° . tan 23 ° . . . . tan 79 ° bằng
A. 9
B. 18
C. 3
D. 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 11 2019
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2021
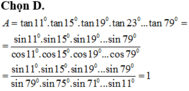
\(tana-cota=2\sqrt{3}\Rightarrow\left(tana-cota\right)^2=12\)
\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)
\(\Rightarrow P=4\)
\(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\)
\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)
\(P=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)
tuỳ ý giá trị biểu thức 
23 tháng 3 2022
a) Ta có: \(sin^2x+sin^2\left(90-x\right)=sin^2x+cos^2x=1.\)
áp dụng: A = 2
b)Ta có: \(cos\left(x\right)=-cos\left(180-x\right)\)
áp dụng: B = 0
c) Ta có: \(tan\left(x\right)\cdot tan\left(90-x\right)=\frac{sinx}{cosx}\cdot\frac{sin\left(90-x\right)}{cos\left(90-x\right)}=\frac{sinx}{cosx}\cdot\frac{cosx}{sinx}=1\)
áp dụng: C = 1
CM
4 tháng 1 2020
Chọn B.
Ta có: A = a.cos2x + 2b.sinx.cosx + c.sin2x
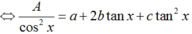
Hay A( 1 + tan2x) = a + 2btanx + c.tan2x
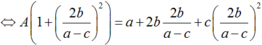
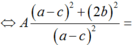
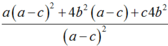
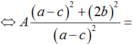
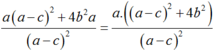
Do đó: A = a.
CM
13 tháng 7 2018
Chọn B.
Ta có
C = ( tan50 . tan 850 ) .( tan 150 tan 750 ) ...tan 450
= ( tan50 .cot 50 ) .( tan 150 cot 150 ) ..tan 450 = 1
( do với 2 góc phụ nhau thì tan góc này bằng cot góc kia)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) \(\tan \left( {a + b} \right) = \frac{{\sin \left( {a + b} \right)}}{{\cos \left( {a + b} \right)}} = \frac{{\sin a.\cos b + \cos a.\sin b}}{{\cos a.\cos b - \sin a.\sin b}}\)
\(\begin{array}{l} = \frac{{\sin a.\cos b + \cos a.\cos b}}{{\cos a.\cos b - \sin a.\sin b}} = \frac{{\sin a.\cos b}}{{\cos a.\cos b - \sin a.\sin b}} + \frac{{\cos a.\sin b}}{{\cos a.\cos b - \sin a.\sin b}}\\ = \frac{{\frac{{\sin a.\cos b}}{{\cos a.\cos b}}}}{{\frac{{\cos a.\cos b - \sin a.\sin b}}{{\cos a.\cos b}}}} + \frac{{\frac{{\cos a.\sin b}}{{\cos a.\cos b}}}}{{\frac{{\cos a.\cos b - \sin a.\sin b}}{{\cos a.\cos b}}}} = \frac{{\tan a}}{{1 - \tan a.\tan b}} + \frac{{\tan b}}{{1 - \tan a.\tan b}}\\ = \frac{{\tan a + \tan b}}{{1 - \tan a.\tan b}}\end{array}\)
\( \Rightarrow \tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a.\tan b}}\)
b)
\(\tan \left( {a - b} \right) = \tan \left( {a + \left( { - b} \right)} \right) = \frac{{\tan a + \tan \left( { - b} \right)}}{{1 - \tan a.\tan \left( { - b} \right)}} = \frac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}\)