Môt lớp có 20 nam sinh và 15 nữ sinh. Giáo viên chọn ngẫu nhiên 4 học sinh lên bảng giải bài tâp. Tính xác suất để 4 hoc sinh được gọi có cả nam và nữ.
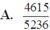
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Số cách chọn 4 học sinh bất kì n Ω = C 35 4 = 52360 (cách).
Số cách chọn 4 học sinh chỉ có nam hoặc chỉ có nữ là C 20 4 + C 15 4 = 6210 (cách).
Do đó số cách chọn 4 học sinh có cả nam và nữ là n A = 52360 − 6210 = 46150 (cách).
Vậy xác suất cần tính là P = n A n Ω = 46150 52360 = 4615 5236 .

Chọn A
Chọn 1 nam trong 20 học sinh nam có C 20 1 cách.
Chọn 1 nữ trong 15 học sinh nữ có C 15 1 cách.
Áp dụng quy tắc nhân có : C 20 1 . C 15 1 = 300 cách.

Chọn C
Số phần tử của không gian mẫu là: ![]() .
.
Gọi biến cố A: “ Hai người được chọn đều là nam”.
![]()
Vậy xác suất cần tìm là: 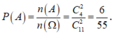 .
.

Số học sinh nữ là:
5564888-2968868=2596020 (học sinh)
Tỉ số % số học sinh nam và học sinh nữ so vơi tổng số học sinh THCS là:
2968868:2596020.100=144,362293%

Số cách chọn 4 học sinh làm 4 tổ trưởng là: ![]()
Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nữ được chọn là ![]()
Số cách chọn 4 học sinh làm tổ trưởng trong đó không có học sinh nam được chọn là: ![]()
Vậy số cách chọn thỏa yêu cầu bài toán: ![]()
Chọn C.

Gọi x là số nhóm có thể chia được nhiều nhất
Theo đề bài , x∈ ƯCLN ( 42; 48) và x >4
42= 2 x 3 x 7
48= 2 x 4 x 3
ƯCLN ( 42 ; 48 )= 2 x 3 = 6
ƯC ( 42; 48 )= Ư( 6 ) = { 1 ; 2 ; 3 ; 6 }
và x>4
⇒ x= 6 nhóm
Vậy có thể chia được thành 6 nhóm
Khi đó mỗi nhóm có :
42 : 6 = 7 ( học sinh nam )
48 : 6 = 8 ( học sinh nữ )
Đ/S : ....
Đáp án A
Số cách chọn 4 học sinh bất kì n ( Ω ) = C 35 4 = 52360 (cách).
Số cách chọn 4 học sinh chỉ có nam hoặc chỉ có nữ là C 20 4 + C 15 4 = 6210 (cách).
Do đó số cách chọn 4 học sinh có cả nam và nữ là n(A) = 52360 - 6210 = 46150 (cách).
Vậy xác suất cần tính là