Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số học sinh nam là x \(\Rightarrow\) nữ là \(30-x\) (\(2\le x< 30\))
Không gian mẫu: \(C_{30}^3\)
Số cách chọn ra 2 nam và 1 nữ: \(C_x^2.C_{30-x}^1\)
Xác suất: \(\frac{C_x^2C_{30-x}^1}{C_{30}^3}=\frac{12}{29}\)
\(\Rightarrow x=16\)
Vậy có 16 nam và 14 nữ

Chọn C
Số phần tử của không gian mẫu là: ![]() .
.
Gọi biến cố A: “ Hai người được chọn đều là nam”.
![]()
Vậy xác suất cần tìm là: 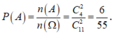 .
.

Đáp án : C
Để chọn một nam và một nữ đi dự trại hè, ta có:
Có 6 cách chọn học sinh khối 12.
Có 3 cách chọn học sinh khối 11.
Có 6 cách chọn học sinh khối 10.
Vậy theo qui tắc nhân ta có 6.3.6=108 cách.

Bạn bị ngược rồi, B có 3 người còn A có 4 người mà. Không sao vẫn tính là bạn đang sắp xếp A nhé, mình kí hiệu 4 học sinh A là A1 A2 A3 A4 thì ở chỗ xếp học sinh A ấy bạn mới chỉ xếp cho A1, A2, A3 hoặc A4 mà thôi nên phải nhân 4 nữa. Đáp án phải là D
D.Công Thiện: Uh mình nhìn nhầm. Nhưng đáp án không thay đổi bạn ơi. Chỉ cần thay B bằng A thôi mà.

S A B C D H M N K
Kẻ \(AH\perp BD\Rightarrow BD\perp\left(SAH\right)\Rightarrow\widehat{SHA}\) là góc giữa (SBD) và (ABCD)
\(\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{AB^2}\Rightarrow AH=\frac{AB.AD}{\sqrt{AB^2+AD^2}}=\frac{a\sqrt{3}}{2}\)
\(SA=\sqrt{SD^2-AD^2}=2a\)
\(tan\widehat{SHA}=\frac{SA}{AH}=\frac{4\sqrt{3}}{3}\Rightarrow\widehat{SHA}\simeq66^035'\)
b/ \(MS=MA\Rightarrow d\left(S;\left(MND\right)\right)=d\left(A;\left(MND\right)\right)\)
Từ A kẻ \(AK\perp MD\Rightarrow AK\perp\left(MND\right)\Rightarrow AK=d\left(A;\left(MND\right)\right)\)
\(AM=\frac{SA}{2}=a\Rightarrow\frac{1}{AK^2}=\frac{1}{AM^2}+\frac{1}{AD^2}\Rightarrow AK=\frac{AM.AD}{\sqrt{AM^2+AD^2}}=\frac{a\sqrt{3}}{2}\)
Chọn A
Chọn 1 nam trong 20 học sinh nam có C 20 1 cách.
Chọn 1 nữ trong 15 học sinh nữ có C 15 1 cách.
Áp dụng quy tắc nhân có : C 20 1 . C 15 1 = 300 cách.