Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 = 3. Một mặt phẳng α tiếp xúc với mặt cầu (S) và cắt các tia Ox, Oy, Oz lần lượt tại A, B, C và thỏa mãn O A 2 + O B 2 + O C 2 = 27. Diện tích của tam giác ABC bằng
A. 3 3 2
B. 9 3 2
C. 3 3
D. 9 3

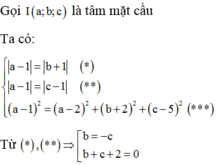
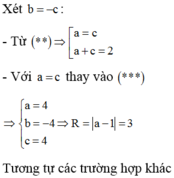
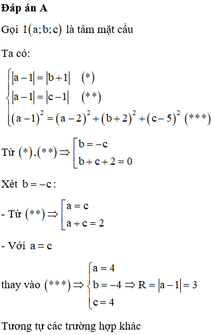
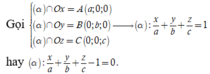







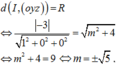
Đáp án B.
Mặt cầu S : x 2 + y 2 + z 2 = 3
có tâm O 0 ; 0 ; 0 và bán kính R = 3
Giả sử A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c với a , b , c > 0 ⇒ Phương trình mặt phẳng α là: x a + y b + z c − 1 = 0
Để ý rằng O A 2 + O B 2 + O C 2 = 27 ⇔ a 2 + b 2 + c 2 = 27 và vì α tiếp xúc mặt cầu S :
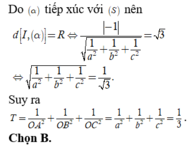
⇒ d O , α = R = 3 ⇔ 0 a + 0 b + 0 c − 1 1 a 2 + 1 b 2 + 1 c 2 = 3 ⇔ 1 a 2 + 1 b 2 + 1 c 2 = 1 3
Ta luôn có bất đẳng thức a 2 + b 2 + c 2 + 1 a 2 + 1 b 2 + 1 c 2 ≥ 9 với a , b , c > 0.
Dấu bằng khi a = b = c = 3
Ta có V O . A B C = O A . O B . O C 6 = a b c 6 = 27 6
hoặc V O . A B C = d O , α . S A B C 3 ⇔ S A B C = 9 3 2 .