Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1 ; 1 ; 1 , B 2 ; 0 ; 1 và mặt phẳng P : x + y + 2 z + 2 = 0. Viết phương trình chính tắc của đường thẳng d đi qua A, song song với mặt phẳng (P) sao cho khoảng cách từ B đến d lớn nhất.
A. d : x − 1 3 = y − 1 1 = z − 1 − 2 .
B. d : x 2 = y 2 = z + 2 − 2 .
C. d : x − 2 1 = y − 2 1 = z − 1 .
D. d : x − 1 3 = y − 1 − 1 = z − 1 − 1 .


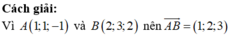

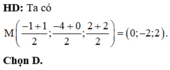

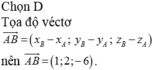

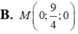
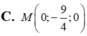


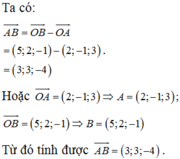
Đáp án C
Gọi (Q) là mặt phẳng qua A và song song với
P ⇒ Q : x + y + 2 z − 4 = 0
Ta có d B ; d ≤ A B ⇒ d B , d max ⇔ AB ⊥ d.
Ta có A B ¯ = 1 ; − 1 ; 0 ⇒ u d ¯ = A B ¯ , n p ¯ = − 2 ; − 2 ; 2
Do đó phương trình đường thẳng d là d : x − 2 1 = y − 2 1 = z − 1 .