Cho ba điểm A, B, C trên giấy kẻ ô vuông ở hình bên. Hãy vẽ điểm thứ tư M sao cho A, B,C, M là 4 đỉnh của một hình bình hành.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
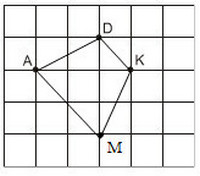
Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM1 (với AK là đáy) và hình thang ADKM2 (với DK là đáy).

a/
Ta có
BE=DF (cạnh đối hbh)
BE=CF (gt)
=> CF=DF => tg CDF cân tại F
Ta có
DF//BE => DF//AB mà \(AB\perp AC\Rightarrow DF\perp AC\)
=> tg CDF vuông cân tại F \(\Rightarrow\widehat{FCD}=\widehat{FDC}=45^o\)
Tg ABC vuông cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}=45^o\)
\(\widehat{BCD}=\widehat{ACF}-\left(\widehat{ACB}+\widehat{FCD}\right)=180^o-\left(45^o+45^o\right)=90^o\)
\(\Rightarrow DC\perp BC\) (đpcm)
b/
Từ E dựng đường thẳng vuông góc với AB cắt BC tại K
Xét tg vuông BEK có
\(\widehat{BKE}=180^o-\left(\widehat{BEK}+\widehat{ABC}\right)=180^o-\left(90^o+45^o\right)=45^o\)
\(\Rightarrow\widehat{ABC}=\widehat{BKE}=45^o\) => tg BEK cân tại E => BE=KE
Mà BE=CF (gt)
=> KE=CF (1)
Ta có
\(KE\perp AB\)
\(AC\perp AB\Rightarrow CF\perp AB\)
=> KE//CF (2)
Từ (1) và (2) => CEKF là hình bình hành (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)
=> IE=IF (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét tg vuông AEF có
IE=IF (cmt) \(\Rightarrow AI=\dfrac{1}{2}EF\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Mà EF=DB (cạnh đối hbh)
\(\Rightarrow AI=\dfrac{1}{2}DB\) (đpcm)
c/ Gọi N là giao của MI với AF
Xét tg vuông CIN có
\(\widehat{CIN}=180^o-\left(\widehat{ACB}+\widehat{MNF}\right)=180^o-\left(45^o+90^o\right)=45^o\)
\(\Rightarrow\widehat{CIN}=\widehat{ACB}=45^o\) => tg CIN cân tại N => NI=NC (3)
\(MI\perp AF;DF\perp AF\) => MI//DF
BD//EF (cạnh đối hbh) => MD//IF
=> DFIM là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => MI=DF
Mà DF=CF (cmt)
=> MI=CF (4)
Xét tg MNF
Từ (3) và (4) \(\Rightarrow\dfrac{NI}{NC}=\dfrac{MI}{CF}=1\) => CI//MF (Talet đảo trong tam giác) (5)
Từ (4) và (5) => MICF là hình thang cân
d/
Nối D với I, Giả sử A; I; D thẳng hàng
DF//BE (cạnh đối hbh) => DF//AB
\(AI=\dfrac{1}{2}EF\) (cmt) mà IE=IF => AI=IE=IF => tg AIE cân tại I
\(\Rightarrow\widehat{EAI}=\widehat{AEI}\) (6)
Mà \(\widehat{EAI}=\widehat{FDI};\widehat{AEI}=\widehat{DFI}\) (góc so le trong) (7)
Từ (6) và (7) \(\Rightarrow\widehat{FDI}=\widehat{DFI}\) => tg IDF cân tại I
=> ID=IF Mà AI=IE=IF => AI=IE=IF=ID
=> AEDF là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Mà \(\widehat{A}=90^o\)
=> AEDF là hcn \(\Rightarrow DE\perp AB\) (8)
=> AD=EF (đường chéo HCN)
mà EF=BD (cạnh đối HCN)
=> AD=BD => tg ABD cân tại D (9)
Từ (8) và (9) => BE=AE (Trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)
=> E phải là trung điểm của AB thì A, I, D thẳng hàng

Gọi AH là chiều cao của tam giác APF.
Ta có: SAPF = AH.PF/2.
a) SPIF = SPAF
⇔ chiều cao IK = AH (Chung cạnh đáy PF).
⇔ I nằm trên đường thẳng song song với PF và cách PF 1 khoảng bằng AH.
b) SPOF = 2.SPAF
⇔ chiều cao OM = 2.AH
⇔ O nằm trên đường thẳng song song với PF và cách PF một khoảng bằng 2.AH
c) 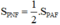
⇔ chiều cao NQ = AH/2
⇔ N nằm trên đường thẳng song song với PF và cách PF một khoảng bằng AH/2.
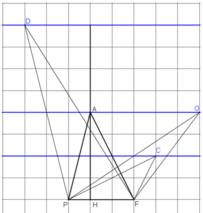

\(a,\Rightarrow C,A,D\) \(thẳng\) \(hàng\Rightarrow\overrightarrow{CA}+\overrightarrow{CD}=\overrightarrow{0}\Leftrightarrow\overrightarrow{CA}=\overrightarrow{DC}\)
\(D\left(x;y\right)\Rightarrow\overrightarrow{CA}=\overrightarrow{DC}\Leftrightarrow\left\{{}\begin{matrix}-1-x=2\\-2-y=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-2\end{matrix}\right.\)\(\Rightarrow D\left(-3;-2\right)\)
\(b,E\left(xo;yo\right)\Rightarrow\overrightarrow{AE}=\overrightarrow{BC}\)\(\Leftrightarrow\left\{{}\begin{matrix}xo-1=-3\\yo+2=-5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}xo=-2\\yo=-7\end{matrix}\right.\)\(\Rightarrow E\left(-2;-7\right)\)
\(c,\Rightarrow G\left(xG;yG\right)\Rightarrow\left\{{}\begin{matrix}xG=\dfrac{1+2-1}{3}=\dfrac{2}{3}\\yG=\dfrac{-2+3-2}{3}=-\dfrac{1}{3}\end{matrix}\right.\)\(\Rightarrow G\left(\dfrac{2}{3};-\dfrac{1}{3}\right)\)

nối BD và AC
trong tam giác ABC ta có: M và N lần luợt là trung đỉêm của AB và AC
=> MN là đuờng trung bình của tam giác ABC
=> MN//AC(
trong tam giác ADC ta có I và K lần luợt là trung điểm của DC và DA
=> KI là đuờng trung bình của tam giác ADC
=> KI//AC
ta có: KI//AC
MN//AC
=> KI//MN(1)
trong tam giác ABD có M và K lần luợt là trung điểm của AB và AD
=> MK là đuờng trung bình của tam giác ADB
=> MK//DB
trong tam giác CDB có I và N lần luợt là trung điểm của DC và CB
=> IN là đuờng trung bình của tam, giác CDB
=>IN//BD
ta có: MK//DB
IN//DB
=> MK//IN(2)
từ (1)(2)=> MK//IN
MN//KI
=> MNIK là hình bình hành
Bài 1:Vẽ đường chéo BD
Xét tam giác ADB có:
M là trung điểm của AB
K là trung điểm của AD
=>KM là đường trung bình của tam giác ADB
=>KM//DB(1) và KM=1/2 DB(3)
Xét tam giác BCD có:
N là trung điểm của BC
I là trung điểm của DC
=>NI là đường trung bình của tam giác BCD
=>NI//DB(2) và NI=1/2DB(4)
Từ (1) và (2)=>KM//NI( //DB)(5)
Từ (3) và (4)=>KM=NI(=1/2 DB)(6)
Từ (5) và (6)=>KMNI là hình bình hành (dhnb3)

a) Cách vẽ:
- Vẽ hình vuông ABCD.
- Vẽ cung tròn tâm A, bán kính là cạnh hình vuông. Cung tròn này đi qua B, D.
- Tương tự với các cung tròn còn lại.
Ta được bốn cung tròn tạo thành hình hoa bốn cánh.
b) Cách vẽ:
- Kẻ lại các ô vuông và lấy các điểm như hình 61.
- Lần lượt vẽ các cung tròn có tâm là các điểm A, B, C, D, E và bán kính là đường chéo của ô vuông.
Ta được năm cung tròn liền nét với nhau tạo thành hình chiếc lọ hoa.

Gọi x (cm) là độ dài đoạn AM.
Điều kiện: 0 < x < 12
Vì ΔABC vuông cân tại A nên ΔBMP vuông cân tại M.
Suy ra MP = MB = AB – AM = 12 – x (cm)
Diện tích hình bình hành MNCP bằng MP.MA = (12 – x)x ( c m 2 )
Theo đề bài, ta có phương trình:
(12 – x)x = 32 ⇔ x 2 – 12x + 32 = 0
∆ ' = - 6 2 – 1.32 = 36 – 32 = 4 > 0
∆ ' = 4 = 2
![]()
Cả hai giá trị của x đều thỏa mãn điều kiện bài toán
Vậy điểm M cách điểm A 8cm hoặc 4cm thì diện tích hình bình hành MNCP bằng 32 c m 2
- Nếu hình bình hành nhận AC làm đường chéo vì AB là đường chéo hình vuông có 2 ô vuông nên C M 1 là đường chéo hình vuông cạnh 2 ô vuông và A, M 1 nằm trên một nửa mặt phẳng bờ BC ta có hình bình hành ABC M 1
- Nếu hình bình hành nhận BC làm đường chéo, điểm A cách điểm C ba ô vuông, điểm B cách điểm M 2 là ba ô vuông và trên một nửa mặt phẳng bờ AB ta có hình bình hành AB M 2 C
- Nếu hình bình hành nhận AB làm đường chéo thì điểm M 3 cách điểm B ba ô vuông, M 3 và A nằm trên cùng một nửa mặt phẳng bờ BC ta có hình bình hành ACB M 3